题目内容
2．观察下列等式：12=1，1+3=22，1+3+5=32，1+3+5+7=42，…，则1+3+5+7+…+2015=10082．分析 据1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，可得1+3+5+…+（2n-1）=n2，据此求出1+3+5+…+2015的值是多少即可．
解答 解：因为1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，
所以1+3+5+…+2015
=1+3+5+…+（2×1008-1）
=10082，
故答案为：10082．
点评 此题主要考查了探寻数列规律问题，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：1+3+5+…+（2n-1）=n2．
练习册系列答案
相关题目
12．
将如图所示的图案平移后得到的图案是（ ）
将如图所示的图案平移后得到的图案是（ ）| A． |  | B． |  | C． |  | D． |  |
13．
如图，方格纸中4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（ ）
如图，方格纸中4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为（ ）| A． | $\frac{1}{2}$π | B． | $\frac{3}{4}$π | C． | $\frac{3}{8}$π | D． | π |
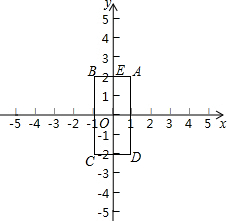如图，已知四边形ABCD的顶点为A（1，2），B（-1，2），C，（-1，-2），D（1，-2），点M和点N同时从E点出发，沿四边形的边做环绕匀速运动，M点以1单位/s的速度做逆时针运动，N点以2单位/s的速度做顺时针运动，则点M和点N第2017次相遇时的坐标为（-1，-1）．
如图，AB∥CD，∠2=3∠1，则∠2=135°．
14．以下列长度的线段为边，能构成直角三角形的是（ ）
| A． | 2，3，4 | B． | 1，1，$\sqrt{2}$ | C． | 5，8，11 | D． | 5，13，23 |
11．把图中的硬纸片沿虚线折叠，不能围成正方体的是（ ）
| A． |  | B． |  | C． |  | D． |  |