题目内容
10.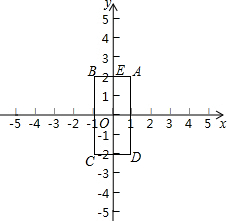 如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C,(-1,-2),D(1,-2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为(-1,-1).
如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C,(-1,-2),D(1,-2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为(-1,-1).
分析 由点A、B、C、D的坐标可得出AB、BC的长度,设点M和点N第2017次相遇时的时间为x,根据第一次相遇的路程和=周长,所以第2017次相遇的路程和=周长×2017,即可得出关于x的一元一次方程,解之即可得出x的值,再根据路程=速度×时间可求出M和点N第2017次相遇时,点M走过的路程,结合矩形的周长为12,即可找出点M和点N第2017次相遇时的坐标,此题得解.
解答 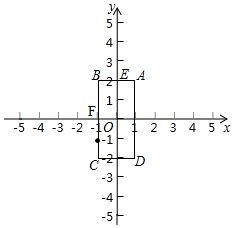 解:∵A(1,2),B(-1,2),C(-1,-2),D(1,-2),
解:∵A(1,2),B(-1,2),C(-1,-2),D(1,-2),
∴AB=2,BC=4.
设点M和点N第2017次相遇时的时间为x,
根据题意得:(1+2)x=2017×2×(4+2),
解得:x=8068,
∴M和点N第2017次相遇时,点M走过的路程为x=8068.
∵矩形ABCD的周长为12,8068=672×12+4,
∴M和点N第2017次相遇时的位置在距离点E逆时针方向的4个单位长度.
∵BC=4,BE=1,
∴点M和点N第2017次相遇时的位置为线段CF的中点,即点(-1,-1).
故答案为:(-1,-1).
点评 本题考查了规律型点的坐标、矩形的周长以及一元一次方程的应用,根据点M走过的总路程结合矩形的周长找出点M和点N第2017次相遇时的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知?ABCD的周长为32,AB=6,则BC等于( )
| A. | 10 | B. | 12 | C. | 24 | D. | 28 |
15.三角形两边长2、3,则最短边x的取值范围是( )
| A. | 1<x<5 | B. | 2<x<3 | C. | 1<x≤2 | D. | 3≤x<5 |
19.已知4x-2y=3,则用x表示y的代数式是( )
| A. | x=$\frac{1}{2}$y+3 | B. | y=$\frac{1}{2}x-\frac{3}{2}$ | C. | y=2x-$\frac{3}{2}$ | D. | x=$\frac{1}{2}y+\frac{3}{4}$ |
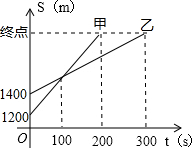 在一次越野赛跑中,甲离出发地1200米,乙离出发地1400米,如图所示,反映的是甲、乙二人离起点的路程S(单位:米)与时间t(单位:秒)之间的关系,那么下列说法中
在一次越野赛跑中,甲离出发地1200米,乙离出发地1400米,如图所示,反映的是甲、乙二人离起点的路程S(单位:米)与时间t(单位:秒)之间的关系,那么下列说法中