题目内容
18.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分面积,可以验证下面一个等式是( )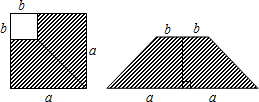
| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | a2+b2=$\frac{1}{2}$[(a+b)2+(a-b)2] |
分析 首先利用正方形的面积,求得左边阴影部分的面积,然后根据梯形的面积公式求得右边阴影部分的面积,根据面积相等即可解答.
解答 解:∵左图中阴影部分的面积是a2-b2,右图中梯形的面积是$\frac{1}{2}$(2a+2b)(a-b)=(a+b)(a-b),
∴a2-b2=(a+b)(a-b).
故选C.
点评 此题主要考查的是平方差公式的几何表示.注意运用不同方法表示阴影部分面积是解题的关键.

练习册系列答案
相关题目
6.数据3.6×10-4用小数表示为( )
| A. | 0.000036 | B. | -0.00036 | C. | 0.00036 | D. | 0.0036 |
13.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )


| A. | (2a2+5a)cm2 | B. | (3a+15)cm2 | C. | (6a+15)cm2 | D. | (8a+15)cm2 |
3.从一个多边形的任何一个顶点出发都只有6条对角线,则它的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
8.不等式组$\left\{\begin{array}{l}{x≥-3}\\{x<5}\end{array}\right.$的解是( )
| A. | -3<x≤5 | B. | x≥-3 | C. | -3≤x<5 | D. | x<5 |
 如图,在直角三角形ABC中,∠C=90°,AC=8,BC=6,设直线1⊥BC,且l从C向B平移,若CH=x,阴影部分面积为y,试求y关于x的函数关系式.
如图,在直角三角形ABC中,∠C=90°,AC=8,BC=6,设直线1⊥BC,且l从C向B平移,若CH=x,阴影部分面积为y,试求y关于x的函数关系式.