题目内容
7．
如图，在直角三角形ABC中，∠C=90°，AC=8，BC=6，设直线1⊥BC，且l从C向B平移，若CH=x，阴影部分面积为y，试求y关于x的函数关系式．
分析 首先求出tanB的值，进而求出DH的长度，利用梯形的面积计算公式求出答案．
解答 解：如图，
∵∠C=90°，AC=8，BC=6，
∴tanB=$\frac{AC}{BC}$=$\frac{4}{3}$，
∵CH=x，
∴BH=6-x，
∴DH=tanB•BH=$\frac{4}{3}$（6-x），
∴阴影部分面积为y=$\frac{1}{2}$（8-$\frac{4}{3}$x+8）x=8x-$\frac{2}{3}$x2．
点评 本题主要考查了平移的知识以及列函数关系式，解题的关键是求出DH的长，此题难度不大．
练习册系列答案
相关题目
17．化简（$\frac{1}{2}$）0的结果为（ ）
| A． | 2 | B． | 0 | C． | 1 | D． | $\frac{1}{2}$ |
18．如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分面积，可以验证下面一个等式是（ ）
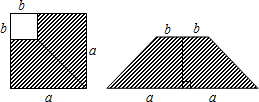
| A． | （a+b）2=a2+2ab+b2 | B． | （a-b）2=a2-2ab+b2 | ||
| C． | a2-b2=（a+b）（a-b） | D． | a2+b2=$\frac{1}{2}$[（a+b）2+（a-b）2] |
15．下列说法正确的是（ ）
| A． | 对角线相等的四边形是矩形 | |
| B． | 对角线互相平分的四边形是平行四边形 | |
| C． | 平行四边形的对角线相等 | |
| D． | 有一个角是直角的四边形是矩形 |
2．要使二次根式$\sqrt{4-x}$有意义，自变量x的取值范围是（ ）
| A． | x＞4 | B． | x＜4 | C． | x≥4 | D． | x≤4 |
如图，已知Rt△ABC中，∠C=90°，∠A=30°．按下列步骤作图：分别以A、B为圆心，以大于$\frac{1}{2}$AB的长为半径作弧，两弧相交于点P和Q作直线PQ，分别交AC于点D，交AB于点E；连接BD．则下列结论中：①AD=BD，②∠CBD=30°③BC=$\frac{1}{2}$AB；④S△ABC=4S△BCD正确的个数有（ ）
19．下列各组线段中，能构成直角三角形的是（ ）
| A． | 1，2，3 | B． | $\sqrt{2}$，$\sqrt{6}$，$\sqrt{3}$ | C． | 1，2，$\sqrt{3}$ | D． | 2，3，5 |
16．已知2x-y=10，则4x-2y+1的值为（ ）
| A． | 10 | B． | 21 | C． | -10 | D． | -21 |
如图，△ABC是等边三角形，AB=6，若点D与点E分别是AB，AC的中点，则DE的长等于3．