题目内容

3．从一个多边形的任何一个顶点出发都只有6条对角线，则它的边数是（　　）
A．6B．7C．8D．9

分析 可根据n边形从一个顶点引出的对角线与边的关系：n-3，列方程求解．

解答 解：设多边形有n条边，
则n-3=6，
解得n=9．
故选：D．

点评 此题主要考查了多边形对角线，多边形有n条边，则经过多边形的一个顶点的所有对角线有（n-3）条，经过多边形的一个顶点的所有对角线把多边形分成（n-2）个三角形．

练习册系列答案
相关题目
13．下列命题中：
①对顶角相等； 
②内错角相等；
③有一条公共边的角叫邻补角；
④经过直线外一点，有且只有一条直线与已知直线平行； 
真命题的个数有（　　）
A．1个B．2个C．3个D．4个
14．若$\sqrt{3}$=a，则$\sqrt{75}$等于（　　）
A．3aB．5aC．15aD．25a
11．已知一个矩形的两条对角线夹角为60°，一条对角线长为10cm，则该矩形的周长为（　　）
A．10（1+$\sqrt{3}$）cmB．20$\sqrt{3}$cmC．20（1+$\sqrt{3}$）cmD．20cm
18．如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分面积，可以验证下面一个等式是（　　）
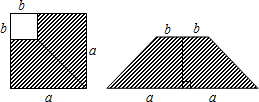
A．（a+b）2=a2+2ab+b2B．（a-b）2=a2-2ab+b2
C．a2-b2=（a+b）（a-b）D．a2+b2=$\frac{1}{2}$[（a+b）2+（a-b）2]
8．将正方形ABCD和正方形EFGB如图1摆放，连结DF．
（1）如图2，将图1中的正方形BEFG绕点B顺时针旋转90°，连接DF、CG相交于点M，请猜想∠DMC的度数并证明；
（2）如图3，将图2中的正方形BEFG绕点B逆时针旋转β角（0°＜β＜90°），连接DF，CG相交于点M，则（1）中的结论是否仍然成立？若成立，请加以证明；若不成立，请说明理由．
15．下列说法正确的是（　　）
A．对角线相等的四边形是矩形
B．对角线互相平分的四边形是平行四边形
C．平行四边形的对角线相等
D．有一个角是直角的四边形是矩形
12．如图，已知Rt△ABC中，∠C=90°，∠A=30°．按下列步骤作图：分别以A、B为圆心，以大于$\frac{1}{2}$AB的长为半径作弧，两弧相交于点P和Q作直线PQ，分别交AC于点D，交AB于点E；连接BD．则下列结论中：①AD=BD，②∠CBD=30°③BC=$\frac{1}{2}$AB；④S△ABC=4S△BCD正确的个数有（　　）
A．1个B．2个C．3个D．4个
13．已知直线的解析式为y=-3x-2，那么该直线的图象不经过（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网