题目内容
9.解方程组:(1)$\left\{\begin{array}{l}{4x-3y=11,①}\\{2x+y=13,②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3x-y=-7,①}\\{y+4z=3,②}\\{2x-2z=-5,③}\end{array}\right.$.
分析 (1)②×2得:4x+2y=26③,再利用③-①可消去未知数x,进而可得y的值,然后再把y的值代入②可计算出x的值,进而可得答案;
(2)首先利用①+②可消去未知数y得3x+4z=-4④,然后再③×2得:4x-4z=-10⑤,再把④⑤组合消去未知数z,计算出x的值,进而可得y、z的值,从而可得方程组的解.
解答 解:(1)②×2得:4x+2y=26③,
③-①得:5y=15,
y=3,
把y=3代入②得:x=5,
方程组的解为$\left\{\begin{array}{l}x=5\\ y=3\end{array}\right.$;
(2)①+②得:3x+4z=-4④,
③×2得:4x-4z=-10⑤,
④+⑤得:7x=-14,
解得:x=-2,
把x=-2代入①得:-6-y=-7,
y=1,
把y=1代入②得:1+4z=3,
z=$\frac{1}{2}$,
方程组的解为$\left\{\begin{array}{l}x=-2\\ y=1\\ z=\frac{1}{2}\end{array}\right.$.
点评 此题主要考查了二元一次方程和三元一次方程组的解,关键是掌握加减消元法解方程组.

练习册系列答案
相关题目
6.在平面直角坐标系中.已知A(0,4).B(-2,0)在坐标轴上确定点P.使△AOP与△AOB相似.则符合条件的点P共有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
1.将一个无盖的正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②),则所剪得直角三角形较短的直角边与较长的直角边的比是 ( )
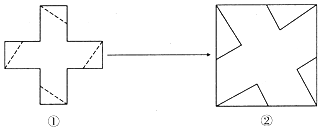

| A. | 1:2 | B. | $\sqrt{3}$:3 | C. | 1:3 | D. | 不能确定 |
19.到三角形的三边距离相等的点是( )
| A. | 三角形三条高的交点 | B. | 三角形三条内角平分线的交点 | ||
| C. | 三角形三条中线的交点 | D. | 无法确定 |
