题目内容
2. 如图,点A、O、B在一条直线上,且∠BOC=120°,OD平分∠AOC,则图中∠AOD=30°°.
如图,点A、O、B在一条直线上,且∠BOC=120°,OD平分∠AOC,则图中∠AOD=30°°.
分析 根据平角的定义求得∠AOC,再由角平分线的定义求∠AOD的度数.
解答 解:∠AOC=∠AOB-∠BOC
=180°-120°
=60°,
∵OD平分∠AOC
∴∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×60°=30°.
故答案为30°.
点评 此题主要考查了平角的定义和角平分线的定义,解决本题的关键是熟记角平分线的定义.

练习册系列答案
相关题目
10.等边三角形面积为8$\sqrt{3}$cm,则它的边长( )
| A. | 2$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 8$\sqrt{2}$cm | D. | 以上结论都不对 |
11.下列各式中,从等号左边变形至等号右边一定成立的是( )
| A. | $\frac{a+b}{{a}^{2}b}$=$\frac{ac+bc}{{a}^{2}bc}$ | B. | $\frac{2x}{{x}^{2}{+y}^{2}}$=$\frac{2x+1}{{x}^{2}{+y}^{2}+1}$ | ||
| C. | $\frac{2x}{{x}^{2}y+xy}$=$\frac{2}{xy+y}$ | D. | $\frac{{x}^{2}{+y}^{2}}{x+y}$=xy |
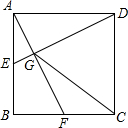 如图,在正方形ABCD中,E,F分别为AB,BC的中点,AF,DE相交于点G,连接CG,则tan∠DGC=2.
如图,在正方形ABCD中,E,F分别为AB,BC的中点,AF,DE相交于点G,连接CG,则tan∠DGC=2. 如图,利用一面墙(长度不限),用24m长的篱笆,围成一个面积为70m2的长方形场地.求长方形的长和宽.
如图,利用一面墙(长度不限),用24m长的篱笆,围成一个面积为70m2的长方形场地.求长方形的长和宽.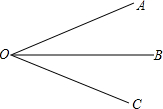 如图∠AOC=60°,OB是∠AOC的平分线,若再把∠AOB四等分,每一份是多少度角(精确到分)?
如图∠AOC=60°,OB是∠AOC的平分线,若再把∠AOB四等分,每一份是多少度角(精确到分)?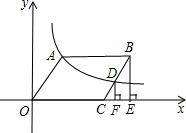 如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.
如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.