题目内容
12.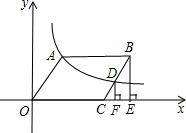 如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.
如图,在平面直角坐标系中,?OABC顶点A,B在第一象限,顶点C在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象过点A,交BC于点D,BE⊥x轴于E,DE⊥x轴于F.设△ODF的面积为S1,四边形BEFD的面积为S2,则S1与S2的大小关系为相等.
分析 根据反比例函数系数k的几何意义,得到S△ODF=$\frac{1}{2}$k,S△AOG=$\frac{1}{2}$K,由四边形OCBA是平行四边形,得到全等三角形,根据等量代换得出∴S△BCE=S△ODF=S1,S2=S△BCE-S△DCF=S1-S△DCF,S1>S2.
解答  解:过点A作AG⊥OC于G,连接OD,
解:过点A作AG⊥OC于G,连接OD,
∵点D在反比例函数的图象上,
∵DF⊥x轴,
∴S△ODF=$\frac{1}{2}$k,
同理S△AOG=$\frac{1}{2}$K,
∵四边形OCBA是平行四边形,
∴AO=BC,AO∥BC,
∴∠AOB=∠BCE,
在△AOG与△BCE中,$\left\{\begin{array}{l}{∠AOG=∠BCE}\\{∠AGO=∠BEC}\\{AO=BC}\end{array}\right.$,
∴△AOG≌△BCE,
∴S△BCE=S△AOG=$\frac{1}{2}$k,
∴S△BCE=S△ODF=S1
∵S2=S△BCE-S△DCF=S1-S△DCF,
∴S1>S2,
故答案为:S1>S2.
点评 本题主要考查反比例函数系数k的几何意义,反比例函数$y=\frac{k}{x}$中k的几何意义,平行四边形的性质,全等三角形的判定与性质,这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.数学家们在研究15、12、10这三个数的倒数时发现:$\frac{1}{12}-\frac{1}{15}=\frac{1}{10}-\frac{1}{12}$,因此就将具有这样性质的三个数称之为调和数,如6、3、2也是一组调和数,现有一组调和数x、5、3(x>5),则x的值是( )
| A. | 15 | B. | 12 | C. | 10 | D. | 20 |
1.如果把分式$\frac{x+2y}{x+y}$中的x和y都扩大10倍,那么分式的值( )
| A. | 扩大10倍 | B. | 缩小10倍 | C. | 是原来的$\frac{2}{3}$ | D. | 不变 |
 如图,点A、O、B在一条直线上,且∠BOC=120°,OD平分∠AOC,则图中∠AOD=30°°.
如图,点A、O、B在一条直线上,且∠BOC=120°,OD平分∠AOC,则图中∠AOD=30°°. 如图是某几何体的三视图,则这个几何体的表面积是3π.
如图是某几何体的三视图,则这个几何体的表面积是3π.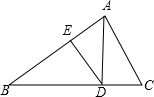 如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )
如图:AD是Rt△ABC斜边BC上的高,DE是△ABD的AB边上的高,则图中与△ABC相似的三角形的个数是( )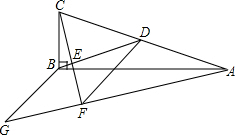 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.