题目内容
7．
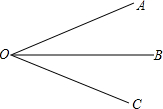如图∠AOC=60°，OB是∠AOC的平分线，若再把∠AOB四等分，每一份是多少度角（精确到分）？
分析 根据角平分线的定义，四等分线的定义即可解答．
解答 解：∵∠AOC=60°，OB是∠AOC的平分线，
∴∠AOB=∠BOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}×6{0}^{°}$=30°．
把∠AOB四等分，每一份是$\frac{1}{4}×3{0}^{°}={7}^{°}3{0}^{′}$．
点评 本题考查的是角平分线的定义，熟知角平分线的定义是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．解方程组：$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{3}=1}\\{2x+3y=\frac{1}{2}}\end{array}\right.$．
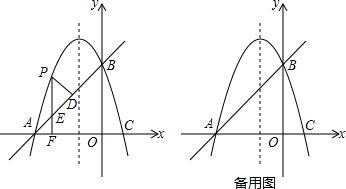
15．与抛物线y=2（x-4）2关于y轴成轴对称关系的抛物线是（ ）
| A． | y=2（x-4）2 | B． | y=-2（x-4）2 | C． | y=2（x+4）2 | D． | y=-2（x+4）2 |
如图，点A、O、B在一条直线上，且∠BOC=120°，OD平分∠AOC，则图中∠AOD=30°°．
16．
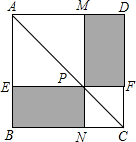如图，在正方形ABCD中，P是线段AC上任意一点，过点P分别作EF∥AD，MN∥AB．设正方形AEPM和正方形CFPN的面积之和为S1，其余部分（即图中两阴影部分）的面积之和为S2，则S1与S2的大小关系是（ ）
如图，在正方形ABCD中，P是线段AC上任意一点，过点P分别作EF∥AD，MN∥AB．设正方形AEPM和正方形CFPN的面积之和为S1，其余部分（即图中两阴影部分）的面积之和为S2，则S1与S2的大小关系是（ ）| A． | S1＞S2 | B． | S1≥S2 | C． | S1＜S2 | D． | S1≤S2 |