题目内容
14.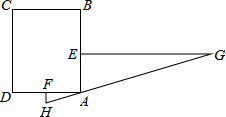 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
分析 首先根据题意得到△GEA∽△AFH,然后利用相似三角形的对应边的比相等列出比例式求得答案即可.
解答 解:∵EG⊥AB,FH⊥AD,HG经过点A,
∴FA∥EG,EA∥FH,
∴∠AEG=∠HFA=90°,∠EAG=∠FHA,
∴△GEA∽△AFH,
∴$\frac{GE}{AF}$=$\frac{AE}{HF}$.
∵AB=9里,AD=7里,EG=15里,
∴AF=3.5里,AE=4.5里,
∴$\frac{15}{3.5}$=$\frac{4.5}{HF}$,
∴FH=1.05里.
点评 本题考查了相似三角形的应用,矩形的性质,解题的关键是从实际问题中整理出相似三角形,难度不大.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
5.滕州市某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
经统计发现两班总数相等,此时有学生建议,可以通过考察数据中的其他信息作为参考,请你回答下列问题:
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
(1)分别求出两班5名学生比赛成绩的中位数;
(2)计算并比较两班比赛数据的方差哪个小?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.
9.某中学生军训,沿着与笔直的铁路并列的公路匀速前进,每小时走4500米,一列火车以每小时120千米的速度迎面开来,测得火车与队首学生相遇,到车尾与队末学生相遇共经过60秒,如果队伍长500米,那么火车长( )
| A. | 1500米 | B. | 1575米 | C. | 2000米 | D. | 2075米 |
 已知:如图,AB平分∠CAD,∠C=∠D.求证:CB=DB.
已知:如图,AB平分∠CAD,∠C=∠D.求证:CB=DB.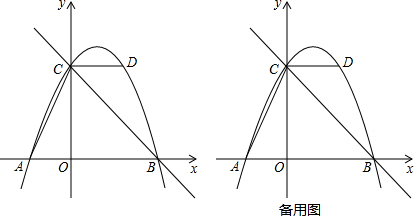
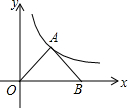 已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.
已知,如图所示,在平面直角坐标系中,Rt△OAB的直角顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,∠AOB=30°,顶点B在x轴上,求此△OAB顶点A的坐标和△OAB面积.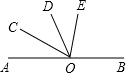 如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数.
如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数.