题目内容
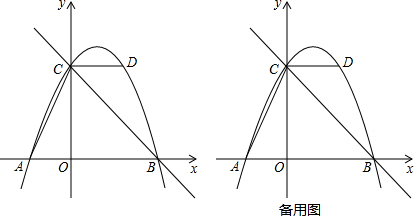
19.如图,抛物线y=ax2+bx+c的图象经过点A(-2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD.(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
分析 (1)设抛物线的解析式为y=a(x-x1)(x-x2),再把点代入即可得出解析式;
(2)分两种情况:①当点E在直线CD的抛物线上方;②当点E在直线CD的抛物线下方;连接CE,过点E作EF⊥CD,再由三角函数得出点E的坐标.
解答  解:(1)∵抛物线y=ax2+bx+c的图象经过点A(-2,0),点B(4,0),点D(2,4),
解:(1)∵抛物线y=ax2+bx+c的图象经过点A(-2,0),点B(4,0),点D(2,4),
∴设抛物线的解析式为y=a(x-x1)(x-x2),
∴y=a(x+2)(x-4),
∴-8a=4,
∴a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x+2)(x-4)=-$\frac{1}{2}$x2+x+4,
(2)①当点E在直线CD的抛物线上方,记E′,连接CE′,过点E′作E′F′⊥CD,垂足为F′,
由(1)得OC=4,
∵∠ACO=∠E′OF′,
∴tan∠ACO=tan∠E′CF′,
∴$\frac{AO}{CO}$=$\frac{E′F′}{CF′}$=$\frac{1}{2}$,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4),
∵点E′在抛物线上,
∴-$\frac{1}{2}$(2h)2+2h+4=h+4,
∴h1=0(舍去),h2=$\frac{1}{2}$,
∴E′(1,$\frac{9}{2}$);
②当点E在直线CD的抛物线下方;
同①的方法得,E(3,$\frac{5}{2}$),
综上,点E的坐标为(1,$\frac{9}{2}$),(3,$\frac{5}{2}$).
点评 本题考查了用待定系数法求二次函数的解析式,掌握二次函数的解析式三种不同的形式是解题的关键.

练习册系列答案
相关题目
9.某乡白梨的包装质量为每箱10千克,现抽取8箱样品进行检测,结果称重如下(单位:千克):10.2,9.9,9.8,10.1,9.6,10.1,9.7,10.2,为了求得8箱样品的总质量,我们可以选取的一个恰当的基准数进行简化运算.
(1)你认为选取的一个恰当的基准数为10千克;
(2)根据你选取的基准数,用正、负数填写上表;
(3)这8箱水果的总质量是多少?
| 原质量(千克) | 10.2 | 9.9 | 9.8 | 9.6 | 10.1 | 9.7 | 10.2 |
| 与基准数的差距(千克) |
(2)根据你选取的基准数,用正、负数填写上表;
(3)这8箱水果的总质量是多少?
 如图,点O为直线AB上一点,过点O作射线OC,已知∠AOC不是直角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.
如图,点O为直线AB上一点,过点O作射线OC,已知∠AOC不是直角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.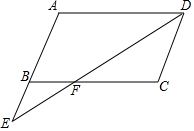 如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.
如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.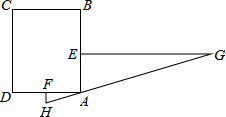 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
 如图,已知数轴上点A表示的数为6,B是数轴上位于点A左侧一点,且AB=22.
如图,已知数轴上点A表示的数为6,B是数轴上位于点A左侧一点,且AB=22.