题目内容
16.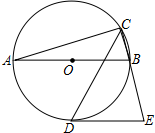 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 如图连接OC、OD,CD与AB交于点F.首先证明∠OFD=60°,再证明∠FOC=∠FCO=30°,求出DF、CF即可解决问题.
解答 解:如图连接OC、OD,CD与AB交于点F.
∵AB是直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴$\widehat{AD}$=$\widehat{DB}$,
∴OD⊥AB,
∵DE是切⊙O切线,
∴DE⊥OD,
∴AB∥DE,∵∠E=75°,
∴∠ABC=∠E=75°,∠CAB=15°,
∴∠CFB=∠CAB+∠ACF=15°+45°=60°,
∴∠OFD=∠CFB=60°,
在RT△OFD中,∵∠DOF=90°,OD=2,∠ODF=30°,
∴OF=OD•tan30°=$\frac{2\sqrt{3}}{3}$,DF=2OF=$\frac{4\sqrt{3}}{3}$,
∵OD=OC,
∴∠ODC=∠OCD=30°,
∵∠COB=∠CAB+∠ACO=30°,
∴∠FOC=∠FCO,
∴CF=FO=$\frac{2\sqrt{3}}{3}$,
∴CD=CF+DF=2$\sqrt{3}$,
故选C.
点评 本题考查了切线的性质,含30°角的直角三角形性质的应用,能求出DF、OF是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
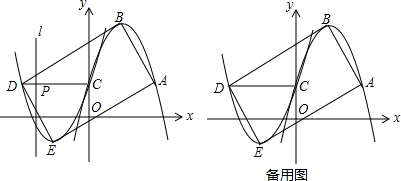
7. 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )| A. | 小亮在图书馆停留的时间是15分钟 | |
| B. | 小亮从学校去图书馆的速度和从图书馆返回学校的速度相同 | |
| C. | 小明离开学校的路程s(千米)与时间t(分)之间的函数关系式为S=$\frac{4}{45}$t | |
| D. | BC段s(千米)与t(分)之间的函数关系式为S=$\frac{4}{45}$t+12 |
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 等腰梯形 |
8.若a<3,则化简$\sqrt{{a^2}-6a+9}$+|4-a|的结果是( )
| A. | -1 | B. | 1 | C. | 2a-7 | D. | 7-2a |