题目内容
8．若a＜3，则化简$\sqrt{{a^2}-6a+9}$+|4-a|的结果是（ ）| A． | -1 | B． | 1 | C． | 2a-7 | D． | 7-2a |
分析 根据二次根式的性质以及绝对值的意义化简即可．
解答 解：∵a＜3，
∴$\sqrt{{a^2}-6a+9}$+|4-a|
=|a-3|+|4-a|
=3-a+（4-a）
=3-a+4-a
=7-2a．
故选D．
点评 本题考查了二次根式的性质和化简，绝对值的意义，合并同类项，比较简单．
练习册系列答案
英才计划期末调研系列答案
相关题目
19．用放大镜观察一个三角形时，不变的量是（ ）
| A． | 各条边的长度 | B． | 各个角的度数 | C． | 三角形的面积 | D． | 三角形的周长 |
16．
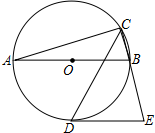如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（ ）
如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 2$\sqrt{3}$ | D． | 3$\sqrt{3}$ |
13．计算（3-π）0+2-1-（-1）3的结果是（ ）
| A． | $\frac{5}{2}$ | B． | $\frac{1}{2}$ | C． | 0 | D． | $\frac{3}{2}$ |
2．
如图，直线m∥n，则90°-∠α为（ ）
如图，直线m∥n，则90°-∠α为（ ）| A． | 70° | B． | 65° | C． | 50° | D． | 40° |
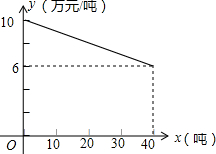某工厂生产一种产品，当生产数量不超过40吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示：