题目内容
10.嘉淇同学计算a+2+$\frac{{a}^{2}}{2-a}$时,是这样做的: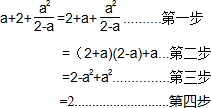
(1)嘉淇的做法从第二步开始出现错误,正确的计算结果应是$\frac{4}{2-a}$;
(2)计算:$\frac{{x}^{2}}{x-1}$-x-1.
分析 (1)根据分式的加减,可得答案.
(2)根据分式的性质,可化成同分母分式,根据分式的加减,可得答案.
解答 解:(1)a+2+$\frac{{a}^{2}}{2-a}$=$\frac{(a+2)(2-a)}{2-a}$+$\frac{{a}^{2}}{2-a}$
=$\frac{4-{a}^{2}+{a}^{2}}{2-a}$
=$\frac{4}{2-a}$,
嘉淇的做法从第 二步开始出现错误,正确的计算结果应是 $\frac{4}{2-a}$,
故答案为:二,$\frac{4}{2-a}$;
(2)$\frac{{x}^{2}}{x-1}$-x-1=$\frac{{x}^{2}}{x-1}$-$\frac{(x-1)(x+1)}{x-1}$=$\frac{{x}^{2}-{x}^{2}+1}{x-1}$=$\frac{1}{x-1}$.
点评 本题考查了分式的加减,通分是分子要加括号,以防错误.

练习册系列答案
相关题目
15.下列问题中,两个变量成正比例的是( )
| A. | 圆的面积S与它的半径r | |
| B. | 正方形的周长C与它的边长a | |
| C. | 三角形面积一定时,它的底边a和底边上的高h | |
| D. | 路程不变时,匀速通过全程所需要的时间t与运动的速度v |
16.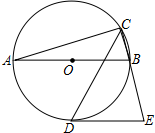 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
13.计算(3-π)0+2-1-(-1)3的结果是( )
| A. | $\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{2}$ |
15.若AB=10,AC=16,且A、B、C三点共线,则AB的中点与AC的中点的距离为( )
| A. | 13 | B. | 3或13 | C. | 3 | D. | 6 |
2. 如图,直线m∥n,则90°-∠α为( )
如图,直线m∥n,则90°-∠α为( )
 如图,直线m∥n,则90°-∠α为( )
如图,直线m∥n,则90°-∠α为( )| A. | 70° | B. | 65° | C. | 50° | D. | 40° |