题目内容
1.(1)计算:($\frac{1}{3-\sqrt{3}}$)0-2cos60°-|$\sqrt{5}$-3|(2)解方程组:$\left\{\begin{array}{l}{2x+y=4}\\{x+2y=5}\end{array}\right.$.
分析 (1)原式利用零指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)原式=1-2×$\frac{1}{2}$-3+$\sqrt{5}$=$\sqrt{5}$-3;
(2)$\left\{\begin{array}{l}{2x+y=4①}\\{x+2y=5②}\end{array}\right.$,
①×2-②得:3x=3,即x=1,
把x=1代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
11.函数y=2x的图象与函数y=-x+1的图象的交点坐标是( )
| A. | (0,1) | B. | (1,0) | C. | (-$\frac{1}{3}$,$\frac{2}{3}$) | D. | ($\frac{1}{3}$,$\frac{2}{3}$) |
12.若3x+1=27,2x=4y-1,则x-y等于( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
16.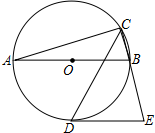 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
6.解方程$\frac{x-1}{x}$-$\frac{2x}{x-1}$=3时,设$\frac{x-1}{x}$=y,则原方程可化为关于y的整式方程是( )
| A. | y-$\frac{2}{y}$=3 | B. | y2-2y=3 | C. | y2-3y-2=0 | D. | y2+3y-2=0 |
13.计算(3-π)0+2-1-(-1)3的结果是( )
| A. | $\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{2}$ |
15.若AB=10,AC=16,且A、B、C三点共线,则AB的中点与AC的中点的距离为( )
| A. | 13 | B. | 3或13 | C. | 3 | D. | 6 |
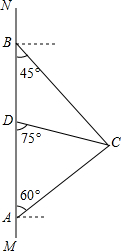 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上. 小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.
小东从甲地出发匀速前往相距20km的乙地,一段时间后,小明从乙地出发沿同一条路匀速前往甲地.小东出发2.5h后,在距乙地7.5km处与小明相遇,之后两人同时到达终点.图中线段AB、CD分别表示小东、小明与乙地的距离y(km)与小东所用时间x(h)的关系.