题目内容
4.下列图形中,既是轴对称图形,又是中心对称图形的是( )| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 等腰梯形 |
分析 结合选项根据轴对称图形与中心对称图形的概念求解即可.
解答 解:A、正三角形是轴对称图形,不是中心对称图形;
B、平行四边形不是轴对称图形,是中心对称图形;
C、矩形是轴对称图形,也是中心对称图形;
D、等腰梯形是轴对称图形,不是中心对称图形.
故选C.
点评 本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形的关键是要寻找对称中心,旋转180度后两部分重合.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
14.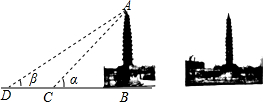 聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )
聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )
 聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )
聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早起,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据:$\sqrt{10}$≈3.162)( )| A. | 15.81米 | B. | 16.81米 | C. | 30.62米 | D. | 31.62米 |
15.下列问题中,两个变量成正比例的是( )
| A. | 圆的面积S与它的半径r | |
| B. | 正方形的周长C与它的边长a | |
| C. | 三角形面积一定时,它的底边a和底边上的高h | |
| D. | 路程不变时,匀速通过全程所需要的时间t与运动的速度v |
12.若3x+1=27,2x=4y-1,则x-y等于( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
19.用放大镜观察一个三角形时,不变的量是( )
| A. | 各条边的长度 | B. | 各个角的度数 | C. | 三角形的面积 | D. | 三角形的周长 |
16.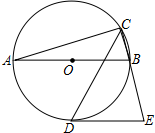 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
13.计算(3-π)0+2-1-(-1)3的结果是( )
| A. | $\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{2}$ |
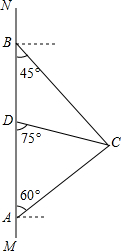 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号,已知A、B两船相距100($\sqrt{3}+1$)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.