题目内容
5. 如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2.
如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2.
分析 根据勾股定理求得AB的长,依据点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$列式计算可得.
解答 解:∵AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,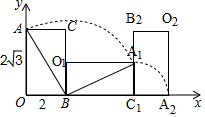
∴点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$
=$\frac{1}{2}$×2$\sqrt{3}$×2+$\frac{90•π•{4}^{2}}{360}$+$\frac{90•π•{2}^{2}}{360}$+$\frac{1}{2}$×2$\sqrt{3}$×2
=4$\sqrt{3}$+5π,
故答案为:(4$\sqrt{3}$+5π)dm2.
点评 本题主要考查轨迹和勾股定理、扇形的面积,根据题意画出图形得出点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列结论中,不能由a+b=0得到的是( )
| A. | a2=-ab | B. | a=0,b=0 | C. | |a|=|b| | D. | a2=b2 |
14.下列运算中,错误的是( )
| A. | $\sqrt{3+5}$=$\sqrt{3}$+$\sqrt{5}$ | B. | $\sqrt{3×5}$=$\sqrt{3}$×$\sqrt{5}$ | C. | $\frac{\sqrt{24}}{\sqrt{6}}$=$\sqrt{\frac{24}{6}}$ | D. | ($\sqrt{2}$)3=2$\sqrt{2}$ |
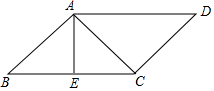 在?ABCD中,AC⊥CD,AE⊥BC.
在?ABCD中,AC⊥CD,AE⊥BC. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长. 如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.
如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,CD=15,AC=17,求△ABC的面积.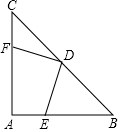 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.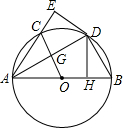 如图,AB为⊙O的直径,点D在⊙O上,DH⊥AB于H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.
如图,AB为⊙O的直径,点D在⊙O上,DH⊥AB于H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.