Question

6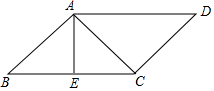．在?ABCD中，AC⊥CD，AE⊥BC．
（1）∠EAC=55°，求∠D的度数；
（2）若AC=8，CD=6，求AE的长．

Answer 1

分析 （1）由平行四边形的性质得出AB=CD，∠B=∠D，AB∥CD，证出AC⊥AB，由直角三角形的性质求出∠BAE=35°，即可得出∠D=∠B=55°；
（2）由勾股定理求出BC，再由直角三角形的面积关系即可求出AE的长．

解答 解：（1）∵四边形ABCD是平行四边形，
∴AB=CD，∠B=∠D，AB∥CD，
∵AC⊥CD，AE⊥BC，
∴AC⊥AB，
∴∠BAE=90°-∠EAC=35°，
∴∠D=∠B=90°-35°=55°；
（2）∵AC⊥AC，AC=8，AB=CD=6，
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10，
∵AE⊥BC，
∴△ABC的面积=$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AE，
∴AE=$\frac{AB×AC}{BC}$=$\frac{6×8}{10}$=4.8．

点评 本题考查了平行四边形的性质、直角三角形的性质、勾股定理以及三角形的面积；熟练掌握平行四边形的性质和勾股定理是解决问题的关键．