题目内容
17.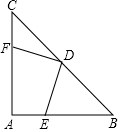 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.(1)求证:DF=DE;
(2)连接EF,若BE=8,CF=6,求△DEF的面积.
分析 (1)连接AD.只要证明△CDF≌△ADE(ASA)即可解决问题.
(2)连接EF,在RT△AEF中,求出FE,再根据等腰直角三角形的性质求出DE、DF即可解决问题.
解答 (1)证明:连接AD.
∵AB=AC,D为BC的中点,
∴AD⊥BC,
又∵∠BAC=90°,
∴AD=CD=BD,∠C=∠DAE=45°,
∵DE⊥DF,
∴∠CDF+∠ADF=∠ADE+∠ADF,
∴∠CDF=∠ADE,
在△CDF和△ADE中
$\left\{\begin{array}{l}∠C=∠DAE\\ CD=AD\\∠CDF=∠ADE\end{array}\right.$,
∴△CDF≌△ADE(ASA),
∴DF=DE.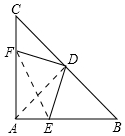
(2)连接EF.由(1)知,AE=CF=6,同理AF=BE=8
∵∠EAF=90°
∴EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵DE=DF,DE⊥DF
∴△DEF为等腰三角形
∴DE2+DF2=EF2=100
∴DE=DF=5$\sqrt{2}$,
∴S△DEF=$\frac{1}{2}$•(5$\sqrt{2}$)2=25.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12.某服装店5400元购进A,B两种童装,按标价全部售出后的总利润是3000元(利润=售价-进价),这两种服装进价、标价如表所示:
(1)求两种童装各购进多少件?
(2)如果A种童装按标价的八折出售,B种童装在标价基础上再降价30元出售.那么这批童装全部售完后,童装店共获得多少利润?
| 类型价格 | A型 | B型 |
| 进价(元/件) | 50 | 80 |
| 标价(元/件) | 80 | 120 |
(2)如果A种童装按标价的八折出售,B种童装在标价基础上再降价30元出售.那么这批童装全部售完后,童装店共获得多少利润?
 如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2.
如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2. 在平面直角坐标系xOy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).(1)作出△ABC关于x轴对称的△A1B1C1,直接写出B1、C1两点的坐标:B1(-2,-3) C1(-3,-1).
在平面直角坐标系xOy中,点A、B、C的坐标分别为(-1,0)、(-2,3)、(-3,1).(1)作出△ABC关于x轴对称的△A1B1C1,直接写出B1、C1两点的坐标:B1(-2,-3) C1(-3,-1). 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,求阴影部分的面积.
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,求阴影部分的面积.