题目内容
14.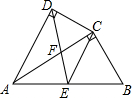 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求$\frac{AC}{AF}$的值.
分析 (1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=AB•AD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=$\frac{1}{2}$AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得$\frac{AC}{AF}$的值.
解答 解:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=AB•AD.
(2)证明:∵E为AB的中点,∠ACB=90°,
∴CE=$\frac{1}{2}$AB=AE.
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
∴AD∥CE;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=$\frac{1}{2}$AB,
∴CE=$\frac{1}{2}$×7=$\frac{7}{2}$,
∵AD=5,
∴$\frac{5}{\frac{7}{2}}$=$\frac{AF}{CF}$,
∴$\frac{AC}{AF}$=$\frac{17}{10}$.
点评 此题考查了相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质,利用直角三角形斜边上中线的性质得到CE=$\frac{1}{2}$AB是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.两圆的半径分别为R和r,圆心距d=3,且R、r是方程x2-7x+10=0的两个根,则这两个圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |
2.从2010年以来,我省中考报名人数逐年递减,2015年全省只有56.65万考生参加中考,其中56.65万用科学记数法表示为( )
| A. | 56.65×104 | B. | 5.665×105 | C. | 5.656×106 | D. | 0.5665×107 |
4.等腰三角形的两边分别为7cm和4cm,则它的周长是( )
| A. | 15cm | B. | 15cm或18cm | C. | 18cm | D. | 11cm |
 如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.
如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.