题目内容
5. 如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.
如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.
分析 根据垂直得出∠FBE=∠ABF=90°,求出∠DBF=∠FBE-∠DBE=40°,∠ABC=∠DBE=50°,即可求出∠CBF.
解答 解:∵BF⊥AE,
∴∠FBE=∠ABF=90°,
∵∠DBE=50°,
∴∠DBF=∠FBE-∠DBE=90°-50°=40°,∠ABC=∠DBE=50°,
∴∠CBF=∠ABF+∠ABC=90°+50°=140°.
点评 本题考查了对顶角、邻补角,垂线的应用,能求出各个角的度数是解此题的关键,注意:数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.如果|-a|=a,则下列a的取值不能使这个式子成立的是( )
| A. | 0 | B. | 1 | C. | 2 | D. | a取任何负数 |
13. 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 两点之间直线最短 | D. | 垂线段最短 |
17. 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )| A. | 7sinα | B. | 7cosα | C. | 7tanα | D. | $\frac{7}{tanα}$ |
15.计算(-4$\frac{7}{8}$)-(+3$\frac{1}{8}$)的结果是( )
| A. | -1$\frac{6}{8}$ | B. | -$\frac{1}{8}$ | C. | -7$\frac{7}{8}$ | D. | -8 |

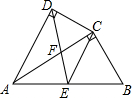 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.