题目内容
3.(1)解方程:x2-4x+3=0;(2)解不等式组$\left\{\begin{array}{l}{3x-1≥x+1}\\{x+4<4x-2}\end{array}\right.$.
分析 (1)方程利用因式分解法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)分解因式得:(x-1)(x-3)=0,
可得x-1=0或x-3=0,
解得:x1=1,x2=3;
(2)$\left\{\begin{array}{l}{3x-1≥x+1①}\\{x+4<4x-2②}\end{array}\right.$,
由①得:x≥1,
由②得:x>2,
则不等式组的解集为x>2.
点评 此题考查了解一元二次方程-因式分解法,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13. 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 两点之间直线最短 | D. | 垂线段最短 |
15.计算(-4$\frac{7}{8}$)-(+3$\frac{1}{8}$)的结果是( )
| A. | -1$\frac{6}{8}$ | B. | -$\frac{1}{8}$ | C. | -7$\frac{7}{8}$ | D. | -8 |
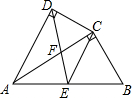 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.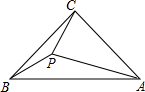 如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.