题目内容
4.等腰三角形的两边分别为7cm和4cm,则它的周长是( )| A. | 15cm | B. | 15cm或18cm | C. | 18cm | D. | 11cm |
分析 分别让4厘米和7厘米的边长当作腰,即可分别求出两种情况下的三角形的周长,从而问题得解.
解答 解:当4厘米的边长为腰时,4厘米、4厘米、7厘米能够构成三角形,三角形的周长为:4×2+7=15(厘米);
当7厘米的边长为腰时,7厘米、7厘米、4厘米能够构成三角形,三角形的周长为:7×2+4=18(厘米).
故它的周长是15厘米或18厘米.
故选:B.
点评 本题考查了等腰三角形的性质,解答此题的关键是:利用假设法,分别求出两种情况下的三角形的周长,问题即可得解.

练习册系列答案
相关题目
15.计算(-4$\frac{7}{8}$)-(+3$\frac{1}{8}$)的结果是( )
| A. | -1$\frac{6}{8}$ | B. | -$\frac{1}{8}$ | C. | -7$\frac{7}{8}$ | D. | -8 |
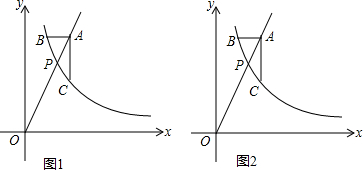
19.在计算器上,有很多按键,有的是运算符号键,有的是数字键,按照如图所示的程序进行操作:如表中的x与y分别是输入的6个数及相应的计算结果
上面操作程序中所按的第三个运算符号键和第四个数字键应是+,1.

| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |

9.下列运算错误的是( )
| A. | $\sqrt{18}$=3$\sqrt{2}$ | B. | 3$\sqrt{2}$×2$\sqrt{3}$=6$\sqrt{6}$ | C. | ($\sqrt{5}$+1)2=6 | D. | ($\sqrt{7}$+2)($\sqrt{7}$-2)=3 |
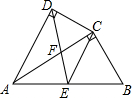 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.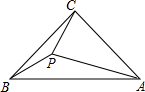 如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.