题目内容
17.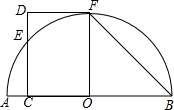 如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°.
如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°.(Ⅰ)求∠D的大小;
(Ⅱ)若OC=CE,BF=2$\sqrt{2}$,求DE的长.
分析 (Ⅰ)首先证明DF∥AB,再根据∠D+∠DCO=180°,DC⊥AB即可解决问题.
(Ⅱ)在RT△BOF中,求出OF,在RT△EOC中求出CE,即可解决问题.
解答 解:(Ⅰ)∵DF是⊙O切线,
∴DF⊥OF,
∴∠DFO=90°,
∵OB=OF,
∴∠OFB=∠B=45°,
∴∠FOB=180°-∠OFB-∠B=180°-45°-45°=90°,
∴∠DFO=∠FOB,
∴DF∥AB,
∴∠D+∠DCO=180°,
∵CD⊥AB,
∴∠DCO=90°,
∴∠D=90°.
(Ⅱ)如图,连接OE,在RT△OBF中,sinB=$\frac{OF}{BF}$,
∴OF=BFsinB=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,
在RT△ECO中,∵OC=CE,设OC=CE=x,
∵OE=OF=2,
∴x2+x2=22,
∴x=$\sqrt{2}$,
∴EC=$\sqrt{2}$,
∵∠D=∠DFO=∠DCO=90°,
∴四边形DCOF是矩形,
∴CD=OF=2,
∴DE=CD-EC=2-$\sqrt{2}$.
点评 本题考查切线的性质、平行线的判定和性质、勾股定理等知识,解题的关键是灵活运用这些知识,属于基础题,中考常考题型.

练习册系列答案
相关题目
8.不等式$\frac{x-1}{2}-\frac{x-2}{4}$>1去分母后得( )
| A. | 2(x-1)-x-2>1 | B. | 2(x-1)-x+2>1 | C. | 2(x-1)-x-2>4 | D. | 2(x-1)-x+2>4 |
2.已知x=m是方程x2-x-2016=0的一个解,则代数式m2-$\frac{2016}{m}$的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
9.下列运算正确的是( )
| A. | x3-3x2=-2x | B. | (-$\frac{1}{3}{x}^{3}$)2=$\frac{1}{9}$x6 | C. | 6x3÷2x-2=3x | D. | (2x-4)2=4x2-16 |
6.下列运算正确的是( )
| A. | (3a)3=9a3 | B. | -x3•(-x)5=x8 | C. | x4+x4=2x8 | D. | (x3)4=x7 |
7.下列运算正确的是( )
| A. | 3-1=-3 | B. | $\sqrt{9}$=±3 | C. | a2+a3=a5 | D. | (ab2)3=a3b6 |
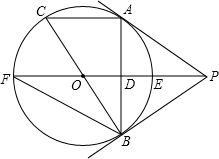 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.