题目内容
12.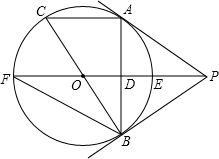 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.(1)求证:PB与⊙O相切;
(2)是探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若tan∠F=$\frac{1}{2}$,求cos∠ACB的值.
分析 (1)先判断出△OAP≌△OBP,再判断出∠OQP=90°即可;
(2)先由射影定理得到OA2=OD×OP,再根据OA=$\frac{1}{2}$EF,代入,化简即可;
(3)根据∠F的正切,设出BD,表示出FD=2a,AD=a,DE=$\frac{1}{2}$a,EF=$\frac{5}{2}$a,得到AC=$\frac{3}{2}$a即可.
解答 解:(1)如图,
连接OA,
∵PD⊥AB,
∴OP垂直平分AB,
∴PA=PB,OA=OB,
∴△OAP≌△OBP,
∴∠OAP=∠OBP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OQP=90°,
∵点B在⊙O上,
∴BP与⊙O相切,
(2)EF,OD,OP间的数量关系为EF2=4OD×OP,
理由:∵∠OAP=90°,AD⊥OP,
∴OA2=OD×OP,
∵OA=$\frac{1}{2}$EF,
∴OD×OP=$\frac{1}{4}$EF2,
∴EF2=4OD×OP,
(3)∵tanF=$\frac{1}{2}$,
设BD=a,
∴FD=2a,AD=a,DE=$\frac{1}{2}$a,EF=$\frac{5}{2}$a,
∴OD=$\frac{3}{4}$a,
∴AC=$\frac{3}{2}$a,
∵BC=EF=$\frac{5}{2}$a
∴cos∠ACB=$\frac{AC}{BC}$=$\frac{\frac{3}{2}a}{\frac{5}{2}a}$=$\frac{3}{5}$.
点评 此题是圆的综合题,主要考查了全等三角形的性质和判定,切线的性质和判定,勾股定理,锐角三角函数,解本题的关键是找出线段间的关系.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.若-x2y=2,则-xy(x5y2-x3y+2x)的值为( )
| A. | 16 | B. | 12 | C. | 8 | D. | 0 |
3.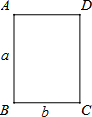 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
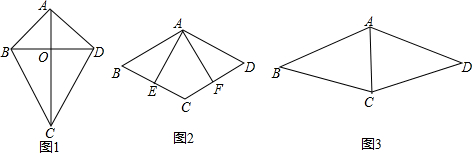
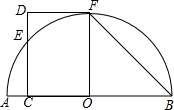 如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°.
如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°. 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.