题目内容
5.用公式法解下列方程.(1)2x2+x+$\frac{1}{4}$=0;
(2)2x2-3x+1=0;
(3)x2-4$\sqrt{3}$+12=0.
分析 (1)先根据根的判别式求出“△”的值,再代入公式求出即可;
(2)先根据根的判别式求出“△”的值,再代入公式求出即可;
(3)先根据根的判别式求出“△”的值,再代入公式求出即可.
解答 解:(1)2x2+x+$\frac{1}{4}$=0,
△=12-4×2×$\frac{1}{4}$=-1<0,
所以此方程无解;
(2)2x2-3x+1=0;
△=(-3)2-4×2×1=1
x=$\frac{3±1}{2×2}$,
x1=1,x2=$\frac{1}{2}$;
(3)x2-4$\sqrt{3}$+12=0,
△=(-4$\sqrt{3}$)2-4×1×12=0
x=$\frac{4\sqrt{3}±0}{2}$,
x1=x2=2$\sqrt{3}$.
点评 本题考查了解一元二次方程的应用,能熟记公式是解此题的关键.

练习册系列答案
相关题目
15. 如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
 如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )| A. | 60cm2 | B. | 72cm2 | C. | 50cm2 | D. | 53cm2 |
16.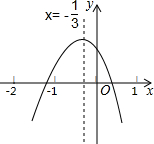 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
①ab>0;
②a+b+c<0;
③b+2c>0;
④点(-3,m),(6,n)都在抛物线上,则有m<n;
你认为其中正确的有( )
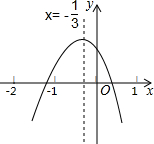 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:①ab>0;
②a+b+c<0;
③b+2c>0;
④点(-3,m),(6,n)都在抛物线上,则有m<n;
你认为其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
10.下列运算中,正确的是( )
| A. | 2xa+xa=3x2a2 | B. | (a2)3=a6 | C. | 3a•2a=6a | D. | 3-2=-6 |
14.计算2×(-3)3+4×(-3)的结果等于( )
| A. | -18 | B. | -27 | C. | -24 | D. | -66 |
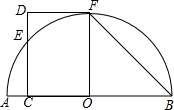 如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°.
如图,AB是半圆O的直径,CD⊥AB于点C,交半圆O于点E,DF切半圆O于点F,∠B=45°.