题目内容
14.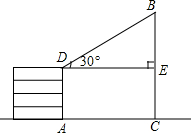 如图,大楼AD高50米,和大楼AD相距90米的C处有一塔BC,某人在楼顶D处测得塔顶B的仰角∠BDE=30°,求塔高.(结果保留整数,参考数据:$\sqrt{2}≈1.41,\sqrt{3}≈1.73$)
如图,大楼AD高50米,和大楼AD相距90米的C处有一塔BC,某人在楼顶D处测得塔顶B的仰角∠BDE=30°,求塔高.(结果保留整数,参考数据:$\sqrt{2}≈1.41,\sqrt{3}≈1.73$)
分析 过点D作DE⊥BC于点E,在直角三角形BDE中,根据∠BDE=30°,求出BE的长度,然后即可求得塔高.
解答 解:过点D作DE⊥BC于点E,
在Rt△BDE中,
∵∠BDE=30°,DE=90米,
∴BE=DE•tan30°=90×$\frac{\sqrt{3}}{3}$=30$\sqrt{3}$(米),
∴BC=BE+EC=BE+AD=30$\sqrt{3}$+50≈102(米).
答:塔高约为102米.
点评 本题考查的是解直角三角形的应用,解答本题的关键是根据仰角构造出直角三角形,利用三角函数的知识求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.2cos30°的值等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
9.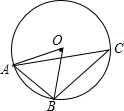 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )| A. | π | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
19.下列运算正确的是( )
| A. | 2a2+a=3a3 | B. | a2÷a=a | C. | (-a)3•a2=-a6 | D. | (3a2)3=9a6 |
6.将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
| A. | y=(x-2)2 | B. | y=x2 | C. | y=x2+6 | D. | y=(x-2)2+6 |
3.化简$(1+\frac{a^2}{1+2a})÷\frac{1+a}{1+2a}$的结果为( )
| A. | 1+a | B. | $\frac{1}{1+2a}$ | C. | $\frac{1}{1+a}$ | D. | 1-a |
4.将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
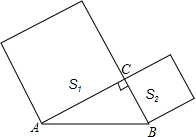 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.