题目内容

4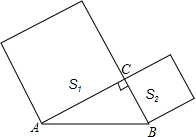．如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为边向外作正方形，面积分别记为S1，S2，则S1+S2的值等于16．

分析 在直角三角形ABC中，利用勾股定理求出AC2+BC2的值，根据S1，S2分别表示正方形面积，求出S1+S2的值即可．

解答 解：∵在Rt△ABC中，∠ACB=90°，AB=4，
∴由勾股定理得：AC2+BC2=AB2=16，
则S1+S2=AC2+BC2=16，
故答案为：16．

点评 此题考查了勾股定理，以及正方形的性质，熟练掌握勾股定理是解本题的关键．

练习册系列答案
相关题目
14．已知抛物线y=x2-3x+m与x轴只有一个公共点，则m=$\frac{9}{4}$．
15．计算
（1）2xy2•（-3xy）2
（2）（2x+y）（2x-y）-3x（x-y）
（3）（$\frac{-a}{b}$）2÷（$\frac{2{a}^{2}}{5b}$）2•$\frac{a}{5b}$．
12．计算：
（1）$|{-1}|-\frac{1}{4}×[{2-{{（-3）}^2}}]$
（2）$-{3^2}+{（-\frac{1}{3}）^2}×{（-3）^3}÷{（-1）^{25}}$．
19．以下列各组线段为边，能组成三角形的是（　　）
A．1cm，2cm，4cmB．4cm，6cm，8cmC．5cm，6cm，12cmD．2cm，3cm，5cm
9．如图，△ABC和△AED是等腰直角三角形，∠BAC=∠EAD=90°，点D、E在∠BAC的外部，连结DC、BE．
（1）求证：BE=CD；
（2）若将△AED绕点A旋转，直线CD交直线AB于点G，交直线BE于点K．若AC=8，GA=2，试求GC•KG的值．
16．某工厂三月份的利润为16万元，五月份的利润为25万元，则平均每月增长的百分率为25%．
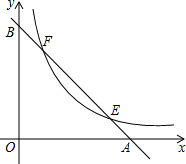13．如图，已知直线y=-x+2分别与x轴，y轴交于A，B两点，与双曲线y=$\frac{k}{x}$交于E，F两点，若AB=2EF，则k的值是$\frac{3}{4}$．
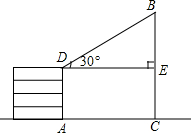14．如图，大楼AD高50米，和大楼AD相距90米的C处有一塔BC，某人在楼顶D处测得塔顶B的仰角∠BDE=30°，求塔高．（结果保留整数，参考数据：$\sqrt{2}≈1.41，\sqrt{3}≈1.73$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网