题目内容
16.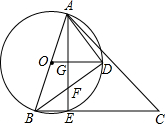 如图,以锐角△ABC的最短边AB的中点O为圆心,AB长为直径作⊙O,交BC于E,连接AE,半径OD⊥弦AE于G,连接AD,BD.
如图,以锐角△ABC的最短边AB的中点O为圆心,AB长为直径作⊙O,交BC于E,连接AE,半径OD⊥弦AE于G,连接AD,BD.(1)若弦AE=12,OG=2.5,求⊙O的半径及弦BE的长;
(2)∠ABF+∠BAF与∠ADF的大小关系,并说明理由;
(3)若$\frac{{{S_{△BFE}}}}{{{S_{△BOD}}}}=\frac{2}{5}$,求$\frac{FB}{AB}$的值.
分析 (1)易证OG是△ABE的中位线,即可得到BE的值,然后在Rt△AEB中运用勾股定理即可求出AB,从而可求出⊙O的半径;
(2)根据圆周角定理可得∠ADB=∠AEB=90°,由此可得∠BFE<∠ADB.根据三角形外角的性质可得∠ABF+∠BAF=∠BFE,即可得到∠ABF+∠BAF<∠ADB;
(3)易证∠OBD=∠ODB=∠DBC,从而可证到△BFE∽△BAD,根据相似三角形的性质可得$\frac{{S}_{△BEF}}{{S}_{△BAD}}$=($\frac{BF}{AB}$)2,要求$\frac{FB}{AB}$的值,只需求$\frac{{S}_{△BEF}}{{S}_{△BAD}}$,由O为AB中点可得S△BOD=$\frac{1}{2}$S△ABD,结合条件即可解决问题.
解答 解:(1)∵OD⊥AE,∴AG=GE.
又∵OA=OB,
∴OG∥BE,OG=$\frac{1}{2}$BE.
∵OG=2.5,∴BE=5.
∵AB是⊙O的直径,∴∠AEB=90°,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∴⊙O的半径为$\frac{13}{2}$,弦BE的长为5;
(2)∠ABF+∠BAF<∠ADB.
理由如下:
∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
∴∠BFE<90°,
∴∠BFE<∠ADB.
∵∠ABF+∠BAF=∠BFE,
∴∠ABF+∠BAF<∠ADB;
(3)∵O为AB中点,
∴S△BOD=$\frac{1}{2}$S△ABD.
∵$\frac{{{S_{△BFE}}}}{{{S_{△BOD}}}}=\frac{2}{5}$,
∴$\frac{{S}_{△BEF}}{{S}_{△BAD}}$=$\frac{1}{5}$.
∵OB=OD,OD∥BE,
∴∠OBD=∠ODB=∠DBC.
又∵∠ADB=∠AEB=90°,
∴△BFE∽△BAD,
∴$\frac{{S}_{△BEF}}{{S}_{△BAD}}$=($\frac{BF}{AB}$)2=$\frac{1}{5}$,
∴$\frac{BF}{AB}$=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了垂径定理、三角形中位线定理、圆周角定理、勾股定理、三角形外角的性质、等腰三角形的性质、平行线的性质、相似三角形的判定与性质等知识,证到△BFE∽△BAD是解决第(3)小题的关键.

| A. | 它的图象关于y轴对称 | |
| B. | 该抛物线开口向下 | |
| C. | 原点是该抛物线上的最高点 | |
| D. | 当x为任意实数时,函数值y总是负数 |
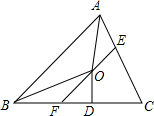 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论: