题目内容
7.解方程(1)x2+4x-1=0(用配方法解方程).
(2)x2-x-1=0.
分析 (1)移项,然后在方程的左右两边同时加上一次项系数一半的平方,左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解.
(2)首先确定a、b、c的值,计算出△的值就可以求出其值.
解答 解:(1)移项,x2+4x=1
x2+4x+4=1+4
(x+2)2=5
∴x+2=±$\sqrt{5}$
解得:x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)原方程变形为:
x2-x-1=0.
∴a=1,b=-1,c=-1,
∴b2-4ac=1-4×(-1)=5.
∴x=$\sqrt{\frac{1±\sqrt{5}}{2}}$
∴x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
点评 本题考查了公式法和配方法解一元二次方程.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
2.多项式(x+2)(2x-1)-2(x+2)可以因式分解成(x+m)(2x+n),则m-n的值是( )
| A. | 2 | B. | -2 | C. | 4 | D. | 5 |
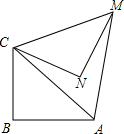 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$.将△ABC绕点C逆时针旋转60°,得到△MNC,则AM的长是2.