题目内容
10．先化简，再求值：（y+1）（2y-3）-（y+1）2-2（y-1）（其中y2-5y=20）分析 原式利用多项式乘以多项式，完全平方式化简，去括号合并得到最简结果，把已知等式代入计算即可求出值．
解答 解：原式=2y2-3y+2y-3-y2-2y-1-2y+2=y2-5y-2，
把y2-5y=20代入得：原式=20-2=18．
点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
14．甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别中A，B两端同时出发，分别到另一端点处掉头，掉头时间不计，速度分别为5m/s和4m/s．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）；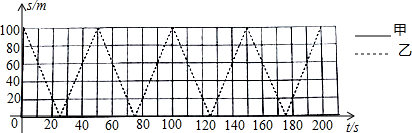
（2）根据（1）中所画图象，完成下列表格：
（3）①直接写出甲、乙两人分别在第一个100m内，s与t的函数解析式，并指出自变量t的取值范围；
②当t=390s时，他们此时相遇吗？若相遇，应是第几次？若不相遇，请通过计算说明理由，并求出此时甲离A端的距离．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）；
（2）根据（1）中所画图象，完成下列表格：
| 两人相遇次数 （单位：次） | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 （单位：m） | 100 | 300 | 500 | 700 | … | 200n-100 |
②当t=390s时，他们此时相遇吗？若相遇，应是第几次？若不相遇，请通过计算说明理由，并求出此时甲离A端的距离．
15．解不等式组$\left\{\begin{array}{l}{4（x+1）≤7x+10}\\{x-5＜\frac{x-8}{3}}\end{array}\right.$，并写出它的所有非负整数解．
12．函数y=$\sqrt{3-x}$+$\frac{1}{x-4}$的自变量x的取值范围是（ ）
| A． | x≤3 | B． | x≠4 | C． | x≥3且x≠4 | D． | x≤3或x≠4 |
15．
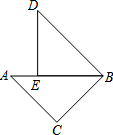如图，△ABC和△DBE都是等腰直角三角形，点E在AB上，若△ABC经旋转后能与△DBE重合，则旋转中心为（ ）
如图，△ABC和△DBE都是等腰直角三角形，点E在AB上，若△ABC经旋转后能与△DBE重合，则旋转中心为（ ）| A． | 点A | B． | 点B | C． | 点C | D． | 点E |
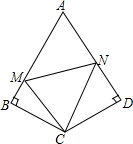如图，四边形ABCD中，∠B=∠D=90°，AB=AD=6，BC=CD，∠BCD=120°，点M、N分别在AB、AD上，且∠MCN=60°．