题目内容
14.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
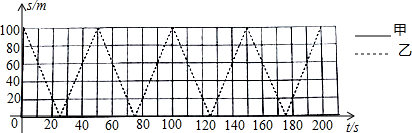
(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数 (单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 (单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
分析 (1)根据甲跑100米所用的时间为100÷5=20(秒),画出图象即可;
(2)根据甲和乙第一次相遇时,两人所跑路程之和为100米,甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),找到规律即可解答;
(3)①根据路程、速度、时间之间的关系即可解答;
②由200n-100=9×390,解得:n=18.05,根据n不是整数,所以此时不相遇,当t=400s时,甲回到A,所以当t=390s时,甲离A端距离为(400-390)×5=50m.
解答 解:(1)如图: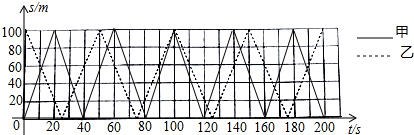
(2)甲和乙第一次相遇时,两人所跑路程之和为100米,
甲和乙第二次相遇时,两人所跑路程之和为100×2+100=300(米),
甲和乙第三次相遇时,两人所跑路程之和为200×2+100=500(米),
甲和乙第四次相遇时,两人所跑路程之和为300×2+100=700(米),
…
甲和乙第n次相遇时,两人所跑路程之和为(n-1)×100×2+100=200n-100(米),
故答案为:500,700,200n-100;
(3)①s甲=5t(0≤t<20),s乙=4t(0≤t≤25).
②由200n-100=9×390,
解得:n=18.05,
∵n不是整数,
∴此时不相遇,
当t=400s时,甲回到A,
当t=390s时,甲离A端距离为(400-390)×5=50m.
点评 本题考查了一次函数的应用,解决本题的关键是相遇问题,第一次相遇100米,以后每次走200米相遇一次,根据所走的路程可求解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
5.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②(m-1)2+(n-1)2≥2;③-1≤2m-2n≤1,其中正确结论的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.下列计算正确的是( )
| A. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | B. | a6÷a3=a2 | C. | (a+b)2=a2+b2 | D. | 2a+3b=5ab |
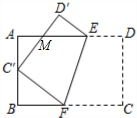 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为$\frac{9}{4}$.
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为$\frac{9}{4}$.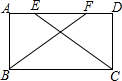 已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.
已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.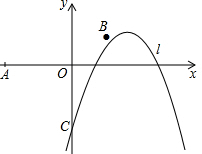 如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.
如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.