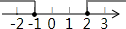题目内容
20.有正面分别标有数字-2、-1、0、1、2的五张不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为m,则使关于x的方程x2+x-m=0有实数解且关于x的不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$有整数解的概率为$\frac{2}{5}$.分析 首先确定使关于x的方程x2+x-m=0有实数解且关于x的不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$有整数解的m的个数,然后利用概率公式求解即可.
解答 解:∵x2+x-m=0有实数解,
∴b2-4ac=1+4m≥0,
∴m≥-$\frac{1}{4}$,
∵解不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$,
∴$\frac{m}{2}$<x<1+2m,
∵关于x的不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$有整数解,
∴m≥0,
∴使关于x的方程x2+x-m=0有实数解且关于x的不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$有整数解的m的值有1,2共2个,
∴P(使关于x的方程x2+x-m=0有实数解且关于x的不等式组$\left\{\begin{array}{l}{2x-m>0}\\{\frac{1}{2}x-\frac{1}{2}<m}\end{array}\right.$有整数解)=$\frac{2}{5}$,
故答案为:$\frac{2}{5}$.
点评 此题考查了概率公式;用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.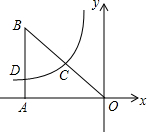 如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
 如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
12.数轴上到原点距离等于5的点有( )
| A. | 5 | B. | -5 | C. | -$\sqrt{5}$ | D. | 5和-5 |