题目内容
16.如图,在Rt△ABC中,AB=BC=6,∠ABC=90°.点P是△ABC外角∠BCN的角平分线上一个动点,点P′是点P关于直线BC的对称点,连结PP′交BC于点M、BP′交AC于点D,连结BP、AP′、CP′.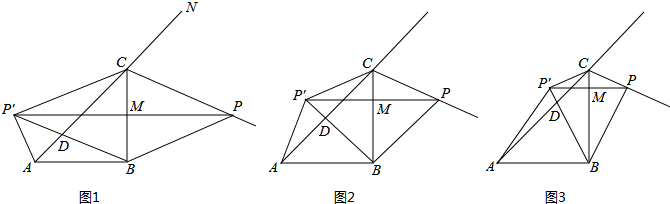
(1)若四边形BPCP′为菱形,求BM的长;
(2)若△BMP′∽△ABC,求BM的长;
(3)若△ABD为等腰三角形,求△ABD的面积.
分析 (1)利用菱形的对角线互相垂直且互相平分进而得出答案;
(2)利用相似三角形的性质得出BM=P′M,∠BMP′=90°,再利用对称的性质以及锐角三角函数关系求出答案;
(3)分别利用当AB=AD时以及当AD=BD时和当AB=BD时求出即可.
解答  解:(1)∵四边形BPCP′为菱形,
解:(1)∵四边形BPCP′为菱形,
∴BM=MC=$\frac{1}{2}$BC=3;
(2)∵△BMP′∽△ABC,AB=BC=6,∠ABC=90°,
∴BM=P′M,∠BMP′=90°,
∵如图2,点P是△ABC外角∠BCN的角平分线上一个动点,点P′是点P关于直线BC的对称点,
∴BP=BP′,∠BCP=∠BPC,
可得AB=BP′=BC=BP=6,
∴BM=sin45°•BP′=$\frac{\sqrt{2}}{2}$×6=3$\sqrt{2}$;
(3)①当AB=AD时,过点D作DE⊥AB,垂足为E,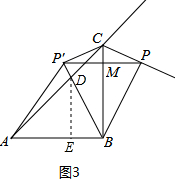
此时△ABD的面积为:$\frac{1}{2}$AB•DE=$\frac{1}{2}$×6×3$\sqrt{2}$=9$\sqrt{2}$;
②当AD=BD时,此时BD⊥AC,△ABD的面积为:$\frac{1}{2}$×$\frac{1}{2}$AB×BC=$\frac{1}{4}$×6×6=9;
③当AB=BD时,此时D,C重合,△ABD的面积为:$\frac{1}{2}$AB•BD=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×6×6=18,
综上所述:△ABD的面积为:9$\sqrt{2}$或9或18.
点评 此题主要考查了菱形的性质以及相似三角形的性质和等腰三角形的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
8.某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( )
| A. | $\frac{20}{81}$ | B. | $\frac{10}{81}$ | C. | $\frac{5}{243}$ | D. | $\frac{10}{243}$ |

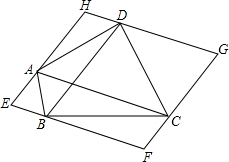 如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH.
如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,得到四边形EFGH. 如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C.
如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C.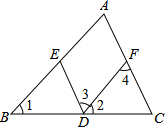 如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.
如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由. 已知,如图,梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,E点是腰AB上的一点,联结CE.
已知,如图,梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,E点是腰AB上的一点,联结CE.