Question

5．已知，如图，梯形ABCD中，AD∥BC，AD=$\frac{1}{3}$BC，E点是腰AB上的一点，联结CE．
（1）如果CE⊥AB，EB=3AE，AB=CD，求∠B的度数；
（2）设S_△BCE=S₁，S_{四边形AECD}=S₂，当S₁=$\frac{3}{2}$S₂时，求$\frac{AE}{EB}$的值．

Answer 1

分析 （1）分别过点A、D作AF⊥BC于点E，作DG⊥BC于点G，连接AC，证明△AFB∽△CEB，根据相似三角形对应边的比相等，以及AB、AD、BE之间的关系求得AB与BF的比值，则∠B的度数即可求解；
（2）设$\frac{AE}{EB}$=a，根据三角形的面积公式，即可得到S1和S2之间的关系，然后根据S₁=$\frac{3}{2}$S₂即可得到关于a的方程，求解即可．

解答 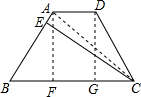解：（1）分别过点A、D作AF⊥BC于点E，作DG⊥BC于点G，连接AC．
∵AD∥BC，AB=CD，
∴四边形ABCD是等腰梯形，
∴BF=CG，
∵AD=$\frac{1}{3}$BC，AD=FG，
∴BF=FG=GC=AD．
∵∠BFC=∠AFB=90°，∠B=∠B，
∴△AFB∽△CEB，
∴$\frac{BA}{BF}=\frac{BC}{BE}$，即$\frac{BA}{AD}=\frac{3AD}{\frac{3}{4}BA}$，
∴3AD²=$\frac{3}{4}$AB²，则$\frac{A{B}^{2}}{B{F}^{2}}=\frac{3}{\frac{3}{4}}=4$，
∴$\frac{AB}{BF}$=2，
∵∠AFB=90°，
∴∠B=30°；
（2）∵AD=$\frac{1}{3}$BC，AD∥BC，
∴$\frac{{S}_{△ABC}}{{S}_{△BEC}}=\frac{AC}{AD}$=3，
∴S_△ABC=3S_△ADC，
设$\frac{AE}{BE}$=a，则$\frac{{S}_{△AEC}}{{S}_{△BEC}}=\frac{AE}{BE}$=a，
$\frac{{S}_{△AEC}+{S}_{△BEC}}{{S}_{BEC}}$=a+1，
$\frac{{S}_{△ABC}}{{S}_{△BEC}}$=a+1，
S_△BEC=$\frac{{S}_{△ABC}}{a+1}$，
∵$\frac{{S}_{△ABC}}{{S}_{△ADC}}$=3，
∴S_△BEC=$\frac{3{S}_{△ADC}}{a+1}$，即S₁=$\frac{3{S}_{△ADC}}{a+1}$，S₂=S_△ADC+S_△AEC=S_△ADC+aS₁，
∵S₁=$\frac{3}{2}$S₂，
∴$\frac{3{S}_{△ADC}}{a+1}=\frac{3{S}_{ADC}+3a{S}_{1}}{2}$，
解得：a=$\frac{1}{4}$．
故$\frac{AE}{EB}$=$\frac{1}{4}$．

点评 本题考查了梯形的性质，以及三角形的面积公式和三角函数，正确进行比例式之间的变化是解决本题的关键．