题目内容
12.计算(1)(4$\sqrt{2}$-3$\sqrt{6}$)$+2\sqrt{2}$
(2)$\sqrt{3}(\sqrt{2}-\sqrt{3})-\sqrt{24}-|\sqrt{6}-3|$
(3)甲、乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如表:
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
分析 (1)去括号合并即可;
(2)先进行二次根式的乘法运算,然后去绝对值合并即可;
(3)先分别计算出甲乙的平均数,然后根据方差公式分别进行甲乙的方差.
解答 解:(1)原式=4$\sqrt{2}$-3$\sqrt{6}$+2$\sqrt{2}$
=2$\sqrt{2}$-3$\sqrt{6}$;
(2)原式=$\sqrt{6}$-3-2$\sqrt{6}$+$\sqrt{6}$-3
=0;
(3)甲的平均数=$\frac{1}{10}$(0+1+0+2+2+0+3+1+2+4)=1.5,
乙的平均数=$\frac{1}{10}$(2+3+1+1+0+2+1+1+0+1)=1.2,
甲的方差=$\frac{1}{10}$×[3×(0-1.5)2+2×(1-1.5)2+3×(2-1.5)2+(3-1.5)2+(4-1.5)2]=16.5;
乙的方差=$\frac{1}{10}$×[2×(0-1.5)2+5×(1-1.5)2+2×(2-1.5)2+(3-1.5)2]=8.5.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了方差.

练习册系列答案
相关题目
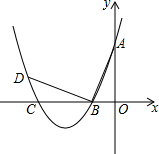 如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
如图,在平面直角坐标系中.顶点为(-4,-1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
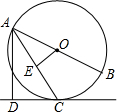 如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.
如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.