题目内容
4.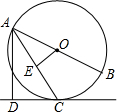 如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.
如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.(1)求证:DC是⊙O的切线;
(2)若OE=$\sqrt{3}$cm,AC=2$\sqrt{13}$cm,求DC的长(结果保留根号).
分析 (1)连接OC,推出∠DAC=∠OCA=∠CAO,推出OC∥AD,推出OC⊥DC,根据切线判定推出即可;
(2)首先求得线段AO的长,然后证△AOE∽△ACD,得出比例式,代入求出即可.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAD,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∴∠ADC=∠OCF,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCF=90°,
∴OC⊥CD,
∵OC为半径,
∴CD是⊙O的切线.
(2)∵OE⊥AC,
∴AE=$\frac{1}{2}$AC=$\sqrt{13}$cm,
在Rt△AOE中,AO=$\sqrt{A{E}^{2}+O{E}^{2}}$=$\sqrt{(\sqrt{13})^{2}+(\sqrt{3})^{2}}$=4cm,
由(1)得∠OAC=∠CAD,∠ADC=∠AEO=90°,
∴△AOE∽△ACD,
∴$\frac{OE}{DC}=\frac{AO}{AC}$,
即$\frac{\sqrt{3}}{DC}=\frac{4}{2\sqrt{13}}$,
∴DC=$\frac{\sqrt{39}}{2}$cm.
点评 本题考查了相似三角形的性质和判定,勾股定理,圆周角定理,平行线性质和判定,等腰三角形性质,切线的判定的应用,主要考查学生的推理能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
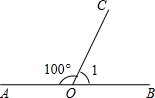 如图,直线AB和OC相交于点O,∠AOC=100°,则∠1=80度.
如图,直线AB和OC相交于点O,∠AOC=100°,则∠1=80度.