题目内容
如图,在抛物线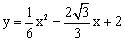 中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: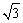 。
。
(1)求m的值;
(2)动点P从B点出发,沿x轴反方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的
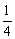 ,求此时点P的坐标。
,求此时点P的坐标。

解 :(1)∵
:(1)∵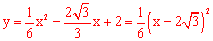 ,
,
∴B(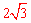 ,0)、A(0,2)、E(
,0)、A(0,2)、E( ,1)。
,1)。
∵CO:OF=2: ,
,
∴CO=﹣m,FO=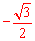 m,
m,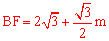 。
。
∵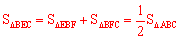 ,
,
∴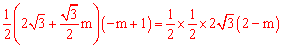 。
。
整理得:m2+m=0。∴m=﹣1或0 。
∵m<0,∴m=﹣1。
(2)在Rt△ABO中,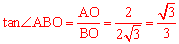 ,
,
∴∠ABO=30°,AB=2AO=4。

①当∠BPE>∠APE时,连接A1B,则对折后如图1,A1为对折后A的所落点,△EHP是重叠部分。

③当∠ BPE<∠APE时.则对折后如图2,A1为对折后A的所落点,△EH
BPE<∠APE时.则对折后如图2,A1为对折后A的所落点,△EH P是重叠部分。
P是重叠部分。
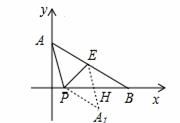
∵E为AB中点,∴S△AEP=S△BEP=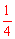 S△ABP。
S△ABP。
∵S△EHP=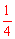 S△ABP,∴S△EBH=S△EHP=
S△ABP,∴S△EBH=S△EHP=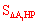 =
=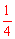 S△ABP。
S△ABP。
∴BH=HP,EH=HA1=1。
又∵BE=EA=2,∴EH
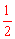 AP。∴AP=2。
AP。∴AP=2。
在△APB中,∠ABP=30°,AB=4,AP=2,
∴∠APB=90°。∴BP=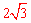 。∴点P的坐标为(
。∴点P的坐标为(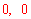 )。
)。
综上所述,点P的坐标为(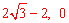 )或(
)或(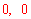 )。
)。
【考点】二次函数综合题,折叠和单动点问题,曲线上点的坐标与方程的关系,锐角三角函数定义,特殊角的三角函数值,平行四边形的判定和性质,二次函数的性质,折叠的性质,分类思想和转换思想的应用。


练习册系列答案
相关题目
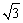
 +1,AD=
+1,AD= 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ; ,将图
,将图 ②中的△AE
②中的△AE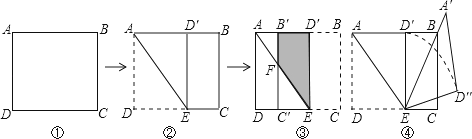
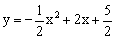 与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。
与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。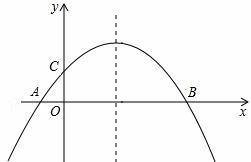
 P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:
P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究: 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
 移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).
移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为________(用含n的代数式表示).

 面积和为S1.
面积和为S1. .
.
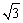 ,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
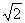 ;
;
 (把所有正确结论序号都填在横线上)。
(把所有正确结论序号都填在横线上)。 比例函数
比例函数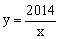 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由; 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式;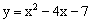 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.