题目内容
如图①,在矩形纸片ABCD中,AB=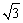
 +1,AD=
+1,AD=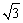
 .
.
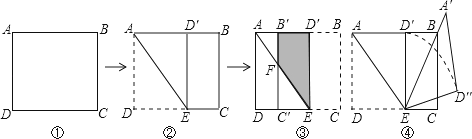
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 ;
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ;
(3)如图④ ,将图
,将图 ②中的△AE
②中的△AE D′绕点E顺时针旋转α角,得△A′ED″,使得EA′
D′绕点E顺时针旋转α角,得△A′ED″,使得EA′ 恰好经过顶点B,求弧D′D″的长.(结果保留π)
恰好经过顶点B,求弧D′D″的长.(结果保留π)
(1)
 。
。
(2)
 。
。
(3)∵∠C=90°,BC=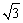
 ,EC=1,∴
,EC=1,∴
 。∴∠BEC=60°。
。∴∠BEC=60°。
由翻折可知:∠DEA=45°,∴∠AEA′=75°=∠D′ED″。
∴

【解析】
 ∵由(1)知AD′=
∵由(1)知AD′=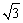
 ,∴BD′=1。
,∴BD′=1。
∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,∴B′D′=BD′=1。
∵由(1)知AD′=AD=D′E=DE=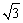
 ,∴四边形ADED′是正方形。
,∴四边形ADED′是正方形。
∴B′F=AB′=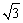
 ﹣1。
﹣1。
∴S梯形B′FED′=
 (B′F+D′E)•B′D′=
(B′F+D′E)•B′D′=
 (
(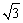
 ﹣1+
﹣1+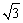
 )×
)× 1=
1=
 。
。
(3)根据直角三角形的性质求出∠BEC的度数,由翻折变换 的性质可得出∠D
的性质可得出∠D EA的度数
EA的度数 ,故可得出∠AEA′=75°=∠D′ED″,由弧长公式即可得出结论。
,故可得出∠AEA′=75°=∠D′ED″,由弧长公式即可得出结论。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目

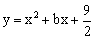 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点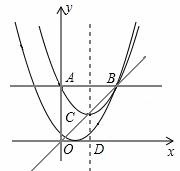
 →BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q
→BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q 两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。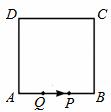
 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
 ,还有 条;
,还有 条;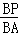
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.


 C值最小时PB的长.
C值最小时PB的长. P逆时针
P逆时针 旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P
旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P CFE
CFE 的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
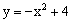 与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。 由。
由。
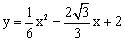 中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: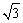 。
。
 ,求此时点P的坐标。
,求此时点P的坐标。