题目内容
已知矩形纸片ABCD中,AB=1,BC=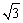 ,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
①当四边形A,CDF为矩形时,EF=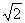 ;
;
②当EF=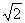 时,四边形A′CDF为矩形;
时,四边形A′CDF为矩形;
③当EF=2时,四边形BA′CD为等腰梯形;
④当四边形BA′CD 为等腰梯形时,EF=2。
为等腰梯形时,EF=2。

其中正确的是  (把所有正确结论序号都填在横线上)。
(把所有正确结论序号都填在横线上)。
①③④。
【考点】折叠问题,折叠对称的性质,矩形的判定和性质,勾股定理,等腰梯形的判定和性质,全等三角形的判定和性质。
【分析】根据相关知识逐一作出判断:
①∵AB=1,BC=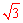 ,
,
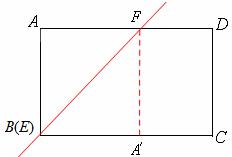
∴如图1,当四边形A′CDF为矩形时,CD= A′F=1,A′F⊥BC。
根据折叠的性质A′E=AB=1。
∴根据勾股定理得EF=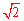 。判断①正
。判断①正 确。
确。
②当EF=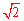 时,由①知,只要E、F分别在边BC、AD上,且E
时,由①知,只要E、F分别在边BC、AD上,且E F与BC成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成矩形。判断②错
F与BC成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成矩形。判断②错 误。
误。
③当EF=2时,
由勾股定理知BD=2,∴此时, EF与BD重合。
EF与BD重合。
由折叠对称和矩形的性质知,CD=AB= A′B,且CD与 A′B不平行。


④当 四边形BA′CD
四边形BA′CD 为等腰梯形时,由A′B=CD,∠A′BD=∠CDB=∠ABD,知点A′是点A关于BD的对称点,即A′是点A沿BD折叠得到,所以,EF与BD重合,EF=BD=2。判断④正确。
为等腰梯形时,由A′B=CD,∠A′BD=∠CDB=∠ABD,知点A′是点A关于BD的对称点,即A′是点A沿BD折叠得到,所以,EF与BD重合,EF=BD=2。判断④正确。
综上所述,判断正确的是①③④。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 P逆时针
P逆时针 旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P
旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P CFE
CFE 的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
 图1,已知直线y=kx与抛物线
图1,已知直线y=kx与抛物线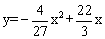
 交于点A(3,6).
交于点A(3,6).

 值?如果是,求出这个定值;如果不是,说明理由;
值?如果是,求出这个定值;如果不是,说明理由; 对称轴右侧的点
对称轴右侧的点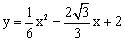 中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: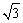 。
。
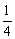 ,求此时点P的坐标。
,求此时点P的坐标。


 00,AB=CB=2,则满足题意的BD长度为整数
00,AB=CB=2,则满足题意的BD长度为整数 的值可以是 (
的值可以是 ( )。
)。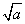
 -
-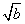
 0,∴a-2
0,∴a-2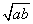
 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 立.
立.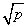
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2
 有最小值 ;
有最小值 ;

 x+1与x轴交于点A,过点A的另一直
x+1与x轴交于点A,过点A的另一直 线L2与双曲线y
线L2与双曲线y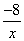

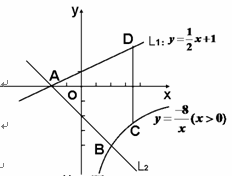

 D,试
D,试
 (x>0
(x>0 )的图象上,过点B1分别作x
)的图象上,过点B1分别作x 轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
 1C1C2B2
1C1C2B2 ;依次在x轴上取点C3(2,0),C4(
;依次在x轴上取点C3(2,0),C4(