题目内容
如图，在平面坐标系中，直线y=﹣x+2与x轴，y轴分别交于点A，点B，动点P（a，b）在第一象限内，由点P向x轴，y轴所作的垂线PM，PN（垂足为M，N）分别与直线AB相交于点E，点F，当点
P（a，b）运动时，矩形PMON的面积为定值2．当点E，F都在线段AB上时，由三条线段AE，EF，BF组成一个三角形，记此三角形的外接圆面积为S1，△OEF的面积为S2．试探究：
是否存在最大值？若存在，请求出该最大值；若不存在，请说明理由．
解：存在。
∴此三角形的外接圆的面积为
。
∵
，
∴S2=S梯形OMPF﹣S△PEF﹣S△OME=
（PF+ON）•PM﹣PF•PE﹣OM•EM
= [PF（PM﹣PE）+OM（PM﹣EM）]= （PF•EM+OM•PE）=PE（EM+OM）
=（a+b﹣2）（2﹣a+a）=a+b﹣2。
∴
。
设m=a+b﹣2，则
，
∵
，∴当
时，
有最大值，最大值为
。
【考点】单动点问题，等腰直角三角形的判定和性质，勾股定理和逆定理，二次函数的性质，偶次幂的非负性质，转换思想的应用。
练习册系列答案
相关题目
→BC→CD向D点运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个单位长度，当P运动到D点时，P、Q
两点同时停止运动。设P点运动的时间为t，△APQ的面积为S，则S与t的函数关系式是 。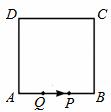
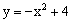与x轴交于点A，与y轴交于点B，动点Q从点O出发，以每秒2个单位长度的速度在线段OA上运动，过点Q作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒。
由。
长；
x， △PDQ的面积为y,求y关于x的函数表达式， 并求自变量的取值范围；
图1，已知直线y=kx与抛物线
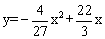
交于点A（3，6）．
值？如果是，求出这个定值；如果不是，说明理由；
对称轴右侧的点
木棒(AB)长为4，斜靠在与地面(OM)垂直的墙壁(ON)上，与地面的倾斜角(∠ABO)为60°，当木棒A端沿N0向下滑动到A′，B端沿直线OM向右滑动到B′，与地面的倾斜角(∠A′
B′O)为45°，则木棒中点从P随之运动到P′所经
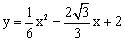中， 抛物线顶点为B，与y轴交于点A，点E为线段AB中点，点C（0，m）是y轴负半轴上一动点，线段EC与线段BO相交于F，且OC：OF=2：
。
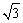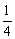，求此时点P的坐标。
00，AB=CB=2，则满足题意的BD长度为整数
的值可以是 （
）。