题目内容
设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反 比例函数
比例函数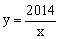 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数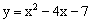 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
解:(1)反比例函数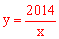 是闭区间[1,20
是闭区间[1,20 14]上的“闭函数”。理由如下:
14]上的“闭函数”。理由如下:
∵反比例函数
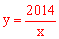 在第一象限,y随x的增大而减小,且
在第一象限,y随x的增大而减小,且
当x=1时,y=2014;当x=2014时,y=1,
∴当1≤x≤201 4时,有1≤y≤2014,符合闭函数的定义,故反比例函数
4时,有1≤y≤2014,符合闭函数的定义,故反比例函数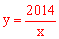 是闭区间[1,2014]上的“闭函
是闭区间[1,2014]上的“闭函 数”。
数”。

(3)∵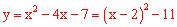 ,
,
∴该二次函数的图象开口方向向上,最小值是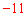 ,且
,且 当x<2时,y随x的增大而减小
当x<2时,y随x的增大而减小 ;当x>2时,y随x的增大而增大。
;当x>2时,y随x的增大而增大。
①当b≤2时,此二次函数y随x的增大 而减小,则根据“闭函数”的定义得,
而减小,则根据“闭函数”的定义得,
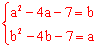 ,两式相减,
,两式相减,
得
∵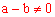 ,∴
,∴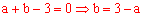 。
。
∴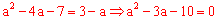
解得, 或
或 (均不合题意,舍去)。
(均不合题意,舍去)。
②当a<2<b时,此时二次函数 的最小值是
的最小值是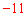 =a,根据“闭函数”的定义得
=a,根据“闭函数”的定义得

【考点】新定义,反比例函数、一次函数和二次函数的性质,解二元方程组,分类思想的应用。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
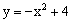 与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。 由。
由。
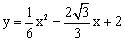 中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2:
中, 抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: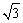 。
。
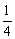 ,求此时点P的坐标。
,求此时点P的坐标。
 00,AB=CB=2,则满足题意的BD长度为整数
00,AB=CB=2,则满足题意的BD长度为整数 的值可以是 (
的值可以是 ( )。
)。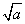
 -
-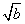
 0,∴a-2
0,∴a-2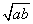
 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2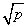
 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2
 有最小值 ;
有最小值 ;

 x+1与x轴交于点A,过点A的另一直
x+1与x轴交于点A,过点A的另一直 线L2与双曲线y
线L2与双曲线y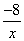

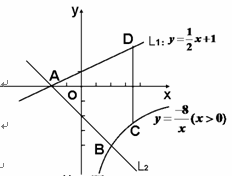

 D,试
D,试
 (x>0
(x>0 )的图象上,过点B1分别作x
)的图象上,过点B1分别作x 轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
 1C1C2B2
1C1C2B2 ;依次在x轴上取点C3(2,0),C4(
;依次在x轴上取点C3(2,0),C4(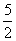
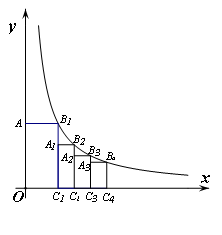

 ,若如果∠1= 那么AB∥EF,若如果∠1=___那么DF∥AC,若∠DEC+___=180°,那么DE∥BC.
,若如果∠1= 那么AB∥EF,若如果∠1=___那么DF∥AC,若∠DEC+___=180°,那么DE∥BC.