题目内容
17.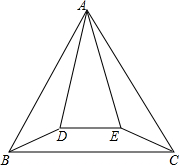 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
分析 由已知条件可证得△ABD≌△ACE,从而得出∠BAD=∠CAE,再由角与角的关系可得出结论.
解答 解:由旋转的性质可知,等腰△ADE的形状不变,位置在变.
①当△ADE在△ABC内时,如图1所示.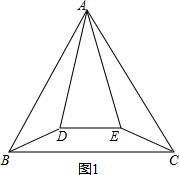
∵△ABC为等边三角形,△ADE为等腰三角形,
∴AB=AC,∠BAC=60°,AD=AE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴∠BAD=∠CAE=$\frac{∠ABC-∠DAE}{2}$=15°;
②当△ADE在△ABC外时,如图2所示.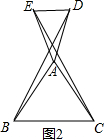
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴∠BAD=∠CAE=$\frac{360°-∠BAC+∠DAE}{2}$=165°.
总上可知:,∠BAD的大小可以是15°、165°.
故答案为:15°或165°.
点评 本题考查了旋转的性质、全等三角形的判定及性质以及角的运算,解题的关键是:由△ABD≌△ACE得出∠BAD=∠CAE.不同属于中档题型,难度不是很大,失分点在于只找到一个结论,即△ADE在△ABC内时的结论,忘记随着旋转,△ADE在△ABC外时也存在满足条件的△ADE.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.下列计算正确的是( )
| A. | x2+x3=2x5 | B. | (-x3)2=-x6 | C. | x6÷x3=x3 | D. | x2•x3=x6 |
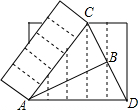 两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.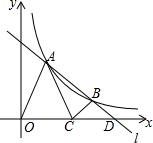 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.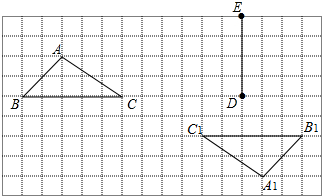 在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.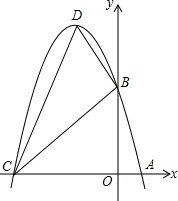 如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.
如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.