题目内容
5.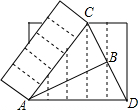 两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
分析 根据题意得出△CBE≌△DBF(AAS),则BC=BD,故S△ABC=S△ADB,进而求出S△ACD,即可得出答案.
解答 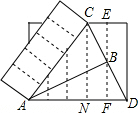 解:如图所示:在△CBE和△DBF中
解:如图所示:在△CBE和△DBF中
∵$\left\{\begin{array}{l}{∠CBE=∠DBF}\\{∠BEC=∠BFD}\\{EC=DF}\end{array}\right.$,
∴△CBE≌△DBF(AAS),
∴BC=BD,
∴S△ABC=S△ADB,
由题意可得:AD=AC=5,AN=3,
则CN=$\sqrt{A{C}^{2}-A{N}^{2}}$=4,
∴S△ADC=$\frac{1}{2}$×4×5=10,
∴S△ABC=S△ADB=5.
故答案为:5.
点评 此题主要考查了勾股定理、全等三角形的判定与性质和三角形面积求法,得出BC=BD是解题关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.如图,用火柴棒搭图形,第1个图形用了三根火柴棒搭出了一个等边三角形,第二个图形在第一个图形的基础上搭了一个每边是一根火柴棒的平行四边形,平行四边形与三角形的公共边只用一根火柴棒,依次交替搭下去搭出以后各个图形,记第n个图形用了an根火柴棒.

(1)填表:
(2)当n为奇数时,小明说:an=5n+3,小亮说:an=$\frac{5n+1}{2}$.你认为他们谁说得对?
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.

(1)填表:
| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.
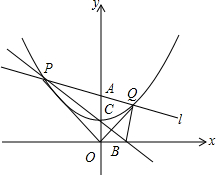 如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).
如图,在直角坐标系中,直线l是绕着定点A(0,2)旋转的动直线,且与经过点C(0,1)的抛物线y=$\frac{1}{4}{x}^{2}+h$交于不同的两点P和Q(即直线l在旋转过程中,不与y轴平行).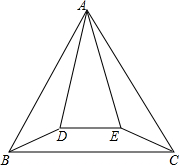 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.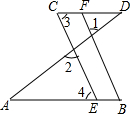 如图,∠3=∠B,∠1=∠2,求证:CD∥AB.
如图,∠3=∠B,∠1=∠2,求证:CD∥AB.