题目内容
7．下列计算正确的是（ ）| A． | x2+x3=2x5 | B． | （-x3）2=-x6 | C． | x6÷x3=x3 | D． | x2•x3=x6 |
分析 根据同底数幂的除法、乘法和幂的乘方，即可解答．
解答 解：A、x2与x3不是同类项，不能合并，故错误；
B、（-x3）2=x6，故错误；
C、x6÷x3=x3，正确；
D、x2•x3=x5，故错误；
故选：C．
点评 本题考查了同底数幂的除法、乘法和幂的乘方，解决本题的关键是熟记同底数幂的除法、乘法和幂的乘方．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18．
如图，直线AB、CD相交于点O，OD平分∠BOE，则∠AOD的补角的个数为（ ）
如图，直线AB、CD相交于点O，OD平分∠BOE，则∠AOD的补角的个数为（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．
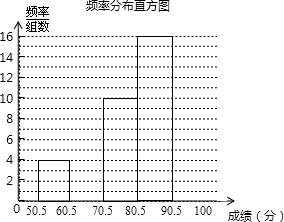6月5日是世界环保日．为了让学生了解环保知识，某中学组织全校2000名学生参加了“环保知识竞赛”．为了解本次竞赛成绩的分布情况，从中抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，得到下面的频率分布表和频数分布直方图．
请根据以上的统计图、表解答下列问题：
频率分布表
（1）补全频率分布表和频数分布直方图；
（2）被抽取的参赛学生中，竞赛成绩落在80.5-90.5分数段的人数最多；
（3）成绩在80分以上为良好，该校所有参赛学生中成绩良好的约为多少人？
6月5日是世界环保日．为了让学生了解环保知识，某中学组织全校2000名学生参加了“环保知识竞赛”．为了解本次竞赛成绩的分布情况，从中抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，得到下面的频率分布表和频数分布直方图．请根据以上的统计图、表解答下列问题：
频率分布表
| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
（2）被抽取的参赛学生中，竞赛成绩落在80.5-90.5分数段的人数最多；
（3）成绩在80分以上为良好，该校所有参赛学生中成绩良好的约为多少人？
用圆规、直尺作图，不写作法，但要保留作图痕迹．
19．为迎接2014年巴西世界杯开幕，某校举办了以欢乐世界杯为主题趣味颠足球比赛：各班代表队所有成员按指定规则同时颠球，成功颠球300个所用时最短的代表队即获胜．预赛中某班的参赛团队每分钟共颠球X个进入决赛，决赛中该团队每分钟颠球的成功率提高为预赛的1.2倍，结果提前了2分钟完成比赛，根据题意，下面所列方程中，正确的是（ ）
| A． | $\frac{300}{1.2x}$$\frac{300}{x}$=2 | B． | $\frac{300}{x}$-$\frac{300}{1.2x}$=2 | C． | $\frac{300}{1.2x}$=$\frac{300}{x-2}$ | D． | $\frac{300}{x+2}$=$\frac{300}{1.2x}$ |
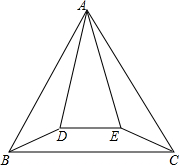如图，正△ABC与等腰△ADE的顶点A重合，AD=AE，∠DAE=30°，将△ADE绕顶点A旋转，在旋转过程中，当BD=CE时，∠BAD的大小可以是15°或165°．