题目内容
12.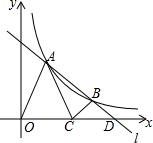 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
分析 作AE⊥x轴于点E,作BF⊥x轴于点F,则△BDF∽△ADE,设A的横坐标是m,纵坐标是n,则mn=k,B坐标可以利用m、n表示,则利用m和n表示出△OAC和△BCD的面积,然后根据S△OAC+S△BCD=2,得到一个关于k的方程,从而求解.
解答  解:作AE⊥x轴于点E,作BF⊥x轴于点F.
解:作AE⊥x轴于点E,作BF⊥x轴于点F.
∵AO=AC,BC=BD,
∴OE=EC,CF=FD,
又∵OC=CD,
∴OE=EC=CF=FD.
∵AE⊥x,BF⊥x,
∴AE∥BF,
∴△BDF∽△ADE,
∴$\frac{BF}{AE}$=$\frac{FD}{DE}$=$\frac{1}{3}$,即BF=$\frac{1}{3}$AE.
设A的横坐标是m,纵坐标是n,则mn=k,B的横坐标3m,纵坐标是$\frac{1}{3}$n.
则S△OAC=$\frac{1}{2}$×2mn=mn=k.S△BCD=$\frac{1}{2}$×2m×$\frac{1}{3}$n=$\frac{1}{3}$mn=$\frac{1}{3}$k.
∵S△OAC+S△BCD=2,
∴k+$\frac{1}{3}$k=2,
解得:k=$\frac{3}{2}$.
故答案是:$\frac{3}{2}$.
点评 本题考查了等腰三角形的性质以及相似三角形的判定与性质,利用k表示出△OAC和△BCD的面积是关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
2.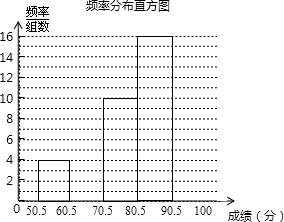 6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
请根据以上的统计图、表解答下列问题:
频率分布表
(1)补全频率分布表和频数分布直方图;
(2)被抽取的参赛学生中,竞赛成绩落在80.5-90.5分数段的人数最多;
(3)成绩在80分以上为良好,该校所有参赛学生中成绩良好的约为多少人?
 6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.请根据以上的统计图、表解答下列问题:
频率分布表
| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
(2)被抽取的参赛学生中,竞赛成绩落在80.5-90.5分数段的人数最多;
(3)成绩在80分以上为良好,该校所有参赛学生中成绩良好的约为多少人?
20.如图,用火柴棒搭图形,第1个图形用了三根火柴棒搭出了一个等边三角形,第二个图形在第一个图形的基础上搭了一个每边是一根火柴棒的平行四边形,平行四边形与三角形的公共边只用一根火柴棒,依次交替搭下去搭出以后各个图形,记第n个图形用了an根火柴棒.

(1)填表:
(2)当n为奇数时,小明说:an=5n+3,小亮说:an=$\frac{5n+1}{2}$.你认为他们谁说得对?
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.

(1)填表:
| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.
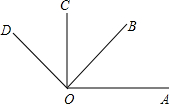 已知∠AOC,∠BOD都是直角,∠BOC=50°
已知∠AOC,∠BOD都是直角,∠BOC=50°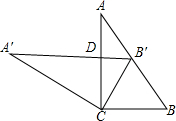 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )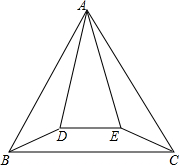 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.