题目内容
如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B；求证：CD⊥AB；
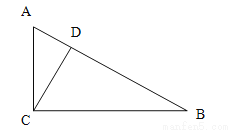
证明过程见解析
【解析】试题分析：根据∠ACB=90°得出∠A+∠B=90°，结合已知条件得出∠A+∠ACD=90°，从而得出答案.
试题解析：∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB
练习册系列答案
相关题目
在△ABC中，若cosA=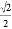
，tanB=
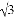，则这个三角形一定是（ ）
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
A
【解析】试题解析：∵cosA=，tanB=，
∴∠A=45°，∠B=60°．
∴∠C=180°-45°-60°=75°．
∴△ABC为锐角三角形．
故选A． 计算：17×3.14＋61×3.14＋22×3.14；
314
【解析】试题分析：根据提公因式法分解因式，先确定公因式3.14，再提取公因式即可.
试题解析：17×3.14＋61×3.14＋22×3.14
=3.14×（17+61+22）
=3.14×100
=314 如图所示，△ABC沿射线MN方向平移一定距离后成为△A′B′C′．找出两个三角形中平行且相等的线段以及全等的三角形．
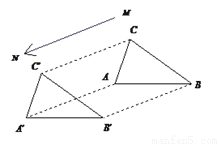
AB、A′B′；BC、B′C′；AC、A′C′；△ABC≌△A′B′C′
【解析】试题分析：根据平移前后两个图形的对应线段平行且相等可以直接找出两个三角形中平行且相等的线段；根据平移前后的两个图形全等可知直接找出全等的三角形．
试题解析：
【解析】
两个三角形中平行且相等的线段有：AB与A’B’，BC与B’C’，AC与A’C’；
全等的三角形是：△ABC≌△A’B’C’．... 如图所示，△DEF是由△ABC经过平移得到的，若∠B=50°,∠C=75°,则∠D=_____，∠E＝________.
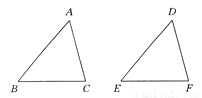
55° 50°
【解析】试题分析：在△ABC中，∠A＝180°－∠B－∠C＝55°，
由平移的性质可知：∠D＝∠A＝55°，∠E＝∠B＝50°，
故答案为：55°，50°． 在一个直角三角形中，有一个锐角等于30°，则另一个锐角的大小为______度．
60
【解析】【解析】
∵三角形是直角三角形，一个锐角等于30°，∴另一个锐角为90°﹣30°=60°．
故答案为：60． 如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（ ）
A. SSS B. AAS C. SAS D. HL
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等，这为“边角边”定理，简写成“SAS”．故选C． 等腰三角形的顶角α＞90°，如果过其顶角的顶点作一条直线将这个等腰三角形分 成了两个等腰三角形，那么α的度数为________．
108°
【解析】如图，
∵AB=AC，BD=AD，AC=CD，
∴∠1=∠B，∠2=∠4，∠B=∠C，
∵∠4=∠1+∠B=2∠B=2∠C，
∴∠2=∠4=2∠C，
∵∠2+∠4+∠C=180°，
∴5∠C=180°，
∴∠C=36°，
∴α=∠BAC=180°-2∠C=108°． 下列各数中，不是不等式2-3x＞5的解的是（ ）
A. -2 B. -3 C. -1 D. -1.35
C
【解析】解不等式2-3x＞5可得x＜-1，因此可知-1不是不等式2-3x＞5的解.
故选：C.