题目内容
12. 如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=$\frac{4}{7}$,△ABD的面积为20,则AD长为$\sqrt{65}$.
如图,四边形ABCD中,AC=AD,2∠ABD+∠CBD=180°,BC=4,tanACB=$\frac{4}{7}$,△ABD的面积为20,则AD长为$\sqrt{65}$.
分析 如图作AE⊥CB于E,AF⊥BD于F.首先证明△ACE≌△ADF,推出CE=DF,∠ACE=∠ADF,设AE=AF=4x,想办法列出方程即可解决问题.
解答 解:如图作AE⊥CB于E,AF⊥BD于F.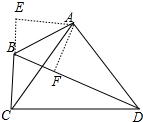
∵2∠ABD+∠CBD=180°,∠CBD+∠ABD+∠ABE=180°,
∴∠ABE=∠ABF,
∴AE=AF,
在Rt△ACE和Rt△ADF中,
$\left\{\begin{array}{l}{AC=AD}\\{AE=AF}\end{array}\right.$,
∴△ACE≌△ADF,
∴CE=DF,∠ACE=∠ADF,设AE=AF=4x,
∵∠tan∠ACE=tan∠ADF=$\frac{4}{7}$,
∴$\frac{AE}{EC}$=$\frac{AF}{DF}$=$\frac{4}{7}$,
∴CE=DF=7x,BE=BF=7x-4,
∵S△ABD=20,
∴$\frac{1}{2}$(7x+7x-4)•4x=20,
∴x=1或-$\frac{5}{7}$(舍弃),
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{{4}^{2}+{7}^{2}}$=$\sqrt{65}$,
故答案为$\sqrt{65}$.
点评 本题考查全等三角形的判定和性质、锐角三角函数、一元二次方程等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
20.“郁郁林间桑葚紫,茫茫水面稻苗青”说的就是味甜汁多,酸甜适口的水果--桑葚,4月份,水果店的小李用3000元购进了一批桑葚,随后的两天他很快以高于进价40%的价格卖出150kg,到了第三天,他发现剩余的桑葚卖相已不大好,于是果断地以低于进价20%的价格将剩余的全部售出,小李一共获利750元,设小李共购进桑葚xkg.
(1)根据题意完成表格填空:(用含x的代数式表示)
(2)求x.
(1)根据题意完成表格填空:(用含x的代数式表示)
| 售价(元/千克) | 销售数量(kg) | |
| 前两天 | ①$\frac{3000}{x}•(1+40%)$ | 150 |
| 第三天 | ②$\frac{3000}{x}•(1-20%)$ | ③x-150 |
 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于D,PE⊥OB于E.若点Q是OC上与O、P不重合的另一点,则以下结论中,一定成立的是①②③(填序号)
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于D,PE⊥OB于E.若点Q是OC上与O、P不重合的另一点,则以下结论中,一定成立的是①②③(填序号) 如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.
如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形. 用一张长方形纸条折成如图所示图形,如果∠1=130°,那么∠2=65°.
用一张长方形纸条折成如图所示图形,如果∠1=130°,那么∠2=65°. 如图,在平面直角坐标系中,点D为x轴上的一点,且点D坐标为(4,0),过点D的直线
如图,在平面直角坐标系中,点D为x轴上的一点,且点D坐标为(4,0),过点D的直线 如图,A,B,C三点都在⊙O上,点D是AB延长线上一点,∠AOC=144°,则∠CBD=72度.
如图,A,B,C三点都在⊙O上,点D是AB延长线上一点,∠AOC=144°,则∠CBD=72度.