题目内容
 如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明
如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明①AB=DE,②∠ABC=∠F,③∠A=∠D,④AC=DF(写出一种即可)
已知:
求证:△ABC≌△DEF.
考点:全等三角形的判定
专题:开放型
分析:选择①④作为条件可利用SSS定理证明△ABC≌△DEF.
解答:解:选择①④作为条件,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
故答案为:①④.
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS).
故答案为:①④.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
相关题目
在同一平面内,连接一个定点和圆上的任意一点的线段中,最短为4cm,最长为9cm,则该圆的半径是( )
| A、2.5cm或6.5cm |
| B、2.5cm |
| C、6.5cm |
| D、5cm或13cm |
已知k1<0<k2,则函数y=k1x和y=
的图象大致是( )
| k2 |
| x |
A、 |
B、 |
C、 |
D、 |
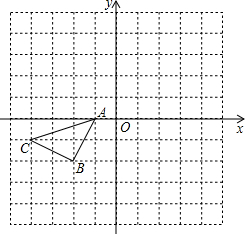 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: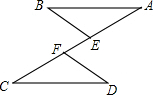 如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是
如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是 长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.
长城家俱雪松路分店为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小强为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.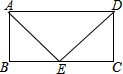 如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为
如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为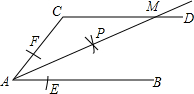 如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于