题目内容
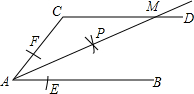 如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
如图,AB∥CD,以点A为圆心,小于AC长为半径画弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于| 1 |
| 2 |
考点:平行线的性质,作图—基本作图
专题:
分析:根据两直线平行,同旁内角互补求出∠BAC,再根据角平分线的定义求出∠BAM,然后根据两直线平行,内错角相等解答.
解答:解:∵AB∥CD,
∴∠BAC=180°-∠C=180°-150°=30°,
由题意得,AP是∠BAC的平分线,
∴∠BAM=
∠BAC=
×30°=15°,
∵AB∥CD,
∴∠CMA=∠BAM=15°.
故答案为:15.
∴∠BAC=180°-∠C=180°-150°=30°,
由题意得,AP是∠BAC的平分线,
∴∠BAM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠CMA=∠BAM=15°.
故答案为:15.
点评:本题考查了平行线的性质,角平分线的定义,熟记性质是解题的关键,难点在于判断出AP是角平分线.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
二次函数y=3x2+mx+6的图象过点A(-3,0),则m的值是( )
| A、3 | B、9 | C、11 | D、-11 |
下列算式中,错误的是( )
| A、1-2=1 |
| B、(-π-3)0=1 |
| C、(-2)-2=0.25 |
| D、0-1=1 |
 如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )| A、∠A=∠B |
| B、AO=BO |
| C、AB=CD |
| D、AC=BD |
 如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明
如图,已知点E,C在线段BF上,BE=CF,请在下列四个等式中,选出两个作为条件,推出△ABC≌△DEF,并予以证明